
Дмитрий Кремнев
Компьютерное моделирование химических взаимодействий
Книга посвящается памяти Александра Арсеньевича Слободова.
Введение
Наш мир построен на законах. Закон всемирного тяготения. Законы электрического и магнитного взаимодействия. Закон сохранения массы и энергии.
Химическое взаимодействие веществ – это одно из основополагающих явлений нашего мира. И оно также подчиняется законам. Невозможно представить себе мир, где вещества бы не реагировали между собой.
Все мы со школьных времен понимаем основы химических взаимодействий. Кислоты реагируют с основаниями с образованием солей и воды. Множество веществ сгорают с образованием оксидов. Растворимые в воде вещества диссоциируют на ионы. Когда количество компонентов, способных вступить в химическое взаимодействие, мало, даже школьнику не составляет большого труда рассчитать результаты таких взаимодействий. Однако с ростом количества компонентов все сильно усложняется.
Задача. Можете ли вы, взглянув на список из 10 веществ, в состав которых входят 12 химических элементов, ответить на вопрос: как прореагирует данная система при температуре в 800°С?
И это не вопрос для проверки уровня знаний на экзамене или способ блеснуть интеллектом в среде химиков. Это один из практических вопросов, которые возникают при разработке новых материалов, создании технологических процессов, в ряде научных исследований.
Один из способов решить такую задачу – провести эксперимент. Смешать вещества, нагреть до нужной температуры и определить состав смеси. Тогда мы столкнемся с рядом трудностей:
• Состав необходимо определить именно при заданной температуре, поскольку при остывании системы в ней могут протекать другие химические превращения, которые поменяют ее состав.
• Если реакции протекают с низкой скоростью, в момент измерения мы можем получить неопределенные данные. Равновесный ли это состав системы? Или продукты попросту еще не успели образоваться?
А если мы захотим изучить влияние различных параметров на процесс? Что изменится при повышении или понижении температуры? Изменении давления? Добавлении новых веществ или изменении количества изначальных?
Экспериментальный подход требует больших материальных и временных затрат, при этом не всегда позволяет получить необходимый результат.
Представьте себе другой подход. Вы вводите в компьютер данные о начальном составе исследуемой системы, температурный интервал, на котором хотите ее изучить, вещества, влияние которых хотите выяснить. И в результате получаете полный расчет: как изменяется состав системы при изменении температуры (какие реакции протекают, какие вещества исчезают и образуются и в каких количествах), как меняется картина происходящего при изменении количественного и качественного состава системы.
Кроме того, вы можете изучить протекание процессов при различных условиях: изобарных, изохорных, в вакууме, при отсутствии возможности образования газов, в воздушной атмосфере. И все это без доступа к дорогостоящему оборудованию и множества потраченных часов и реагентов.
Именно этому подходу и посвящена данная книга. Главная наша задача – упростить исследования сложных многокомпонентных систем, предоставить методологию и инструменты, способные облегчить получение в простом и наглядном виде картины происходящих химических процессов и способов влияния на них.
Целью внедрения расчетных методов мы видим появление новых технологических процессов, новых материалов, а также новых, более оптимальных составов и условий производства существующих. И, как следствие, ускорение темпов научно-технического прогресса, улучшение конкурентоспособности и качества российской продукции.
В любой книге (и наша – не исключение) могут присутствовать опечатки и прочие ошибки. По мере их обнаружения мы будем пополнять их список на странице slobodovreactor.ru/spisok-ispravlenij/.
Для того чтобы быть с нами в контакте, запустите нашего бота в Телеграм: @slobodov_reactor_bot.
История появления метода

Все началось с математики. Александр Арсеньевич Слободов окончил матмех ЛГУ в 1976 году и поступил на работу в ЛСХИ на кафедру математики. И вскоре был задействован на кафедре химии для обработки экспериментальных данных.
В 1980 году Александр Арсеньевич перешел в Технологический институт, где его выдающиеся математические способности также пригодились в области обработки данных экспериментов на кафедре Физической химии и послужили основой для докторской диссертации одного из сотрудников кафедры.
Через несколько лет работы с различными экспериментальными данными возникла идея: а что, если попытаться смоделировать сложные эксперименты термодинамическими расчетами? С этого момента начал складываться аппарат термодинамического моделирования.
Первые программы работали на ЭВМ Минск-22 и БЭСМ-4 на языках Алгол и Фортран. По мере появления более совершенных ЭВМ происходил переход программного комплекса на языки более высокого уровня. Методы термодинамического моделирования показали свою эффективность и экспериментальное подтверждение, в результате чего продолжали развиваться.
Одним из первых внешних заказчиков стала Ленинградская АЭС. Расчеты протекающих физико-химических превращений в контурах охлаждения как в штатных режимах работы, так и в экстремальных позволили лучше понять происходящие процессы и, как следствие, выработать алгоритмы действий во внештатных ситуациях.
Позже метод нашел применение в области производства люминофорных композиций, компонентность которых делала практически невозможным изучение фазово-химических превращений при их синтезе как с точки зрения эксперимента, так и с помощью простых расчетных методов. В результате были найдены причины и методы борьбы с браком продукции, оптимизированы рецептурные составы.
Также метод нашел свое применение в расчетах процесса синтеза стекол, керамики, азотных удобрений и многих других процессов.
В результате более чем четырех десятилетий использования данного подхода к моделированию различных многокомпонентных систем в широкой области параметров состояния, было принято решение сделать его доступным для широкого круга научных, технических и технологических специалистов в нашей стране.
Так появилась сперва идея, а затем и реализация сервиса SlobodovReactor. Поскольку программная часть метода была адаптирована под старые, практически вышедшие из эксплуатации системы, автору книги пришлось с нуля писать программную реализацию для облачной архитектуры системы.
Сервис только начал свое развитие. Пока на нем присутствуют только самые необходимые функции. Но мы нацелены на его скорейшее развитие и повсеместное внедрение.
К великому сожалению, 11.07.2023 ушел из жизни Александр Арсеньевич. Однако дело его продолжает жить. Надеемся, что благодаря сервису, носящему его имя, профессор Слободов останется в памяти научного сообщества одним из великих русских ученых, внесшим большой вклад в области термодинамического моделирования.
Расчет химического равновесия
Равновесие – это цель, к которой стремится по крайней мере вся неживая природа. Шарик под действием гравитации будет катиться по наклонной поверхности до тех пор, пока не достигнет равновесия. Качели рано или поздно остановятся, если их не раскачивают. Наполненный легким газом шар поднимется на такую высоту, где все силы, действующие на него, будут компенсированы.
Химическое взаимодействие не является исключением. Аналогом потенциальной энергии физического объекта, стремящегося к своему равновесному состоянию, в случае химических взаимодействий является свободная энергия системы. Система стремится к такому состоянию, при котором свободная энергия будет минимальной.
Постановка и решение задачи
Движущая сила химических процессов, протекающих в системах, – уменьшение свободной энергии этих систем. Например, для наиболее распространенных изобарно-изотермических условий эту роль играет энергия Гиббса.
В системе, находящейся первоначально в неравновесном состоянии, могут протекать различные химические реакции, в результате которых будут образовываться различные химические вещества.
Общая энергия Гиббса системы складывается из энергий Гиббса всех веществ, которые в нее входят. Другими словами, она является функцией числа молей входящих в нее веществ, а также давления и температуры.
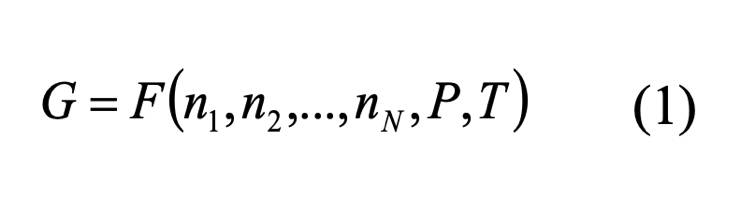
В итоге, при заданных параметрах состояния в системе образуются такие вещества и в таких количествах, при которых энергия системы становится минимальной. Наша задача заключается в том, чтобы определить, что это за вещества и каковы их количества. Для этого нам нужно найти минимум функции, выражающей энергию Гиббса системы.
Поскольку в точке минимума функции многих переменных частные производные по всем переменным обращаются в ноль, то составим систему уравнений:

Так как G(n1, … , nN) – экстенсивная функция, т. е. является однородной первого порядка, то по теореме Эйлера имеем:
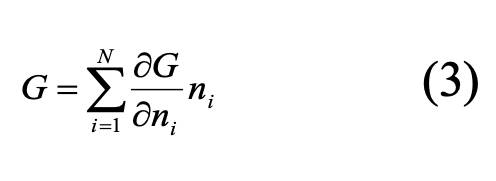
С другой стороны, из определения химического потенциала:

В нашем случае на решение данной системы накладываются условия материального баланса: количество вещества в системе должно оставаться постоянным. Это значит, что искать минимум функции надо не во всей области существования, а в той области, которая задается ограничениями. Функция в этом случае достигает минимума в точке экстремума (если он лежит в этой области), либо на границе области.
Поясним на примере. Рассмотрим систему, образованную из двух химических веществ: SO2 и N2.
Эта система состоит из трех химических элементов: S, O и N. В результате взаимодействия из этих веществ могут образоваться любые вещества, состоящие из этих трех элементов: оксиды серы и азота, соединения серы и азота и, наконец, соединения серы, азота и кислорода. Составим матрицу {ai,j}MxN материального баланса для этих веществ:
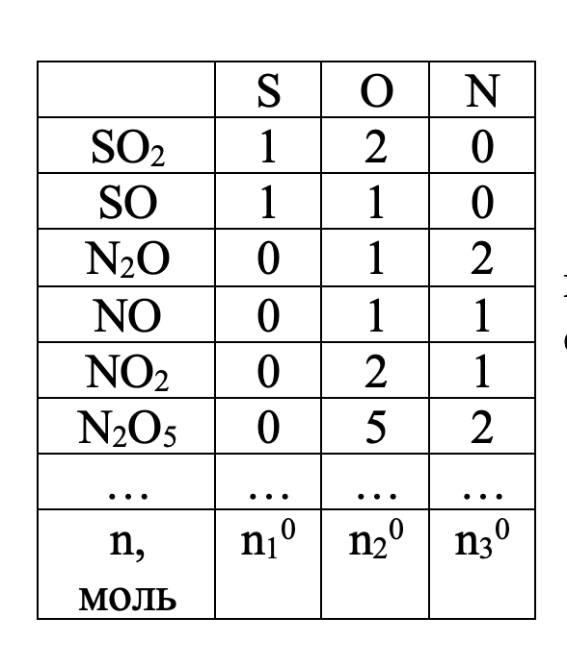
Запишем материальный баланс системы в следующем виде:

Где nj0 – количество молей элемента j, которое определяется количеством веществ, из которых первоначально состояла система; M – количество химических элементов в системе.
Кроме того, на решение нашей задачи накладывается еще одно условие: равновесные количества веществ не должны быть отрицательными. Наша система уравнений и неравенств примет следующий вид:

Таким образом, решив данную систему, мы определим количества веществ, образующихся в системе, когда она приходит в состояние равновесия.
В общем случае химический потенциал складывается из:
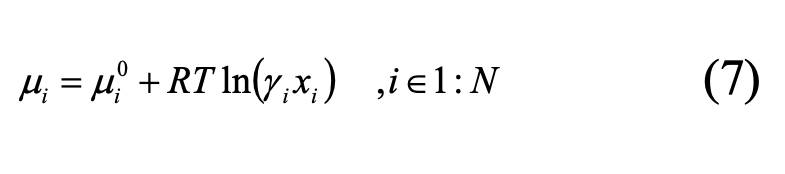
Рассмотрим случай, когда вещества в системе существуют в индивидуальном состоянии, то есть не растворяются друг в друге. В этом случае в уравнении (7) второй член станет равным нулю, и химический потенциал любого вещества в системе будет равен его энергии Гиббса. Назовем расчет равновесного состава системы, состоящей из индивидуальных веществ (фаз), фазовым расчетом.
Сущность решения заключается в определении коэффициентов функции в области, определяемой набором равенств и неравенств таким образом, чтобы значение функции было минимальным. В результате этого расчета мы будем иметь набор ni, то есть равновесные количества веществ в системе.
В случае, когда вещества в системе образуют растворы, необходимо учитывать их активности при расчете химического потенциала.
В результате решения этой задачи мы также получим набор ni (i=1…N) – количество каждого вещества, образующегося в системе, когда она приходит в состояние равновесия [1].
Описанный подход можно назвать термодинамическим моделированием равновесного состава. Он является той самой базой, на которой строятся расчеты фазово-химических взаимодействий.
Второй неотъемлемой частью является набор термодинамических характеристик веществ, как изначально входящих в исследуемую систему, так и способных образовываться в систему в результате их взаимодействия и изменения параметров состояния системы.


