
Гарет Мур
Тренажер мозга. Продвинутый уровень: 40 дней интенсивных тренировок
День 3
Путь короля
+ Заполнить все клетки поля числами начиная с 1 (конечное число зависит от размера поля в головоломке)
+ Числа должны идти в порядке возрастания
ПРАВИЛА
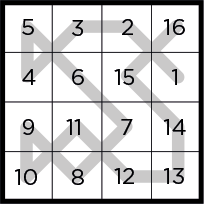
Заполните все клетки поля числами от 1 (конечное число зависит от размера поля в головоломке). Числа должны быть размещены так, чтобы образовать непрерывный «путь» от 1 до наибольшего числа, возрастая на единицу в каждом шаге. Числа не должны повторяться. Разрешенные шаги соответствуют ходам короля в шахматах – то есть влево, вправо, вверх, вниз или по диагонали на соседние клетки.
МЫСЛИТЕЛЬНЫЙ ПРОЦЕСС
В процессе решения этой головоломки часто надо делать догадки и корректировать их по мере дальнейшего решения, пока количество вариантов в каждой клетке не будет сведено до единственно возможного числа. Это отличный пример пошаговой оптимизации, когда первоначальное предположение постепенно уточняется и доводится до совершенства.

УЧЕБНЫЙ ТРЕНАЖЕР
Нарисуйте «путь короля» от 1 до 16 в задаче 1 и от 1 до 36 в задаче 2.
• Чтобы определить начало и конец пути, обычно нужно поломать голову, но в задачах в этой главе они обозначены. Кроме начальной и конечной клеток, во всех остальных случаях путь должен входить в каждую клетку и выходить из нее. Поскольку угловые клетки и в меньшей степени клетки по краям более ограничены в вариантах, чем клетки в середине поля, решение головоломки лучше начинать с них, когда это возможно.
• Поищите числа, разделенные одним числом. Можно ли поместить число между ними в единственно возможную клетку?
• Также поищите числа, которые разделены максимально возможным количеством клеток, – например, числа, отстоящие друг от друга на три числа, между которыми находится три клетки. В этом случае путь должен пролегать по прямой от одного числа к другому. Однако чем дальше друг от друга отстоят числа, тем больше между ними возможных маршрутов. Вы можете проложить между ними предполагаемый путь (пометив, что это предположение, а не окончательный вариант) и, отталкиваясь от этого, работать дальше.
УЧЕБНЫЙ ТРЕНАЖЕР

Разместите в сетке числа от 1 до 64.
• Помните, что король может двигаться по диагонали. Если забыть об этом, головоломка может показаться неразрешимой, тогда как из кажущегося тупика есть простой выход.
• Заполняя поле, постоянно проверяйте пустые клетки. Можно ли провести через них путь и, если да, будет ли он соединять числа в соответствии с правилами? Если нет, значит, нужно исправить те части пути, которые вы уже проложили.
• Если какая-то область поля вызывает затруднение, оставьте ее и займитесь другой – проложенная там часть пути может в итоге затронуть эту трудную область и подсказать ее решение.
ПОПРОБУЙТЕ СВОИ СИЛЫ

Разместите на поле числа от 1 до 100.
День 4
Лабиринт
+ Найти путь от входа до выхода
ПРАВИЛА
Проложите путь через лабиринт, следуя по белым коридорам и не пересекая черные стены.

МЫСЛИТЕЛЬНЫЕ ПРОЦЕССЫ
Лабиринт – одна из старейших известных головоломок, которая была описана еще в древнегреческой мифологии более 3000 лет назад. Прохождение настоящих больших лабиринтов – невероятно сложное дело, потому что в них очень трудно ориентироваться и отслеживать свое местоположение. Но с нарисованными лабиринтами все гораздо проще. Решение этих головоломок требует не столько логических рассуждений, сколько разумных догадок, хотя если решать их «в уме», не прочерчивая путь на бумаге, то также нужна устойчивая зрительная концентрация и хорошая память, чтобы не повторять один и тот же тупиковый путь. Можно использовать и тактические приемы – например, исходя из предположений о том, как был спроектирован лабиринт, попробовать пройти его в обратном направлении, что может быть намного проще, но некоторые считают такое решение «нечестным».

УЧЕБНЫЙ ТРЕНАЖЕР

• Если путь в лабиринте не может проходить по разным уровням – например, по мостам или разным этажам, – тогда простая тактика решения состоит в том, чтобы исключить все «тупиковые» области. Другими словами, когда вы обнаруживаете область, полностью изолированную либо краями лабиринта, либо ранее выявленными «тупиковыми» областями – то есть теми, из которых нет выхода, – ее не нужно больше обследовать. Иногда это может значительно упростить оставшуюся часть лабиринта, поэтому постарайтесь намеренно двигаться к краям лабиринта, чтобы попытаться исключить из него как можно больше тупиковых областей.
ПОПРОБУЙТЕ СВОИ СИЛЫ


В этом лабиринте путь может проходить по мостам и под мостами.
День 5
Судоку
+ Расставить цифры так, чтобы они не повторялись в строках, столбцах и блоках
ПРАВИЛА
Заполните сетку цифрами от 1 до 6 (количество цифр зависит от размера сетки) так, чтобы ни одна цифра не повторялась ни в одной строке, столбце или блоке, очерченном жирной линией.

МЫСЛИТЕЛЬНЫЕ ПРОЦЕССЫ
Судоку, пожалуй, самая популярная из всех логических головоломок. Она редко бывает разочаровывающе простой или, наоборот, удручающе сложной настолько, чтобы не поддаваться решению. Решение этой головоломки доставляет истинное удовлетворение (помимо естественного удовольствия от заполнения пустых клеток). Несмотря на простые правила, она требует использования очень разнообразной логики вместе с десятками различных методов решения.

УЧЕБНЫЙ ТРЕНАЖЕР

• Самая простая тактика в судоку – найти цифру, которая может находиться в единственно возможном месте в данной области (в строке, столбце или блоке). Например, в блоке 3 × 2 посередине слева есть всего одно место, где может располагаться цифра 1.
• Противоположная тактика – найти клетку в данной области, которая может содержать только одну возможную цифру, – гораздо сложнее. В этом случае полезно делать пометки карандашом – записывать в каждой клетке маленькие цифры, которые могут здесь находиться. Но не следует делать на сетке слишком много карандашных пометок, потому что иначе вы перестанете видеть лес за деревьями!
• Проверяйте линии пересечения. Кроме того, если цифра может находиться только в одной конкретной строке или столбце данного блока, значит, она не может находиться в той же строке или столбце в других блоках. Это мощный метод исключения, поэтому при обнаружении такой комбинации полезно делать соответствующие карандашные пометки.
УЧЕБНЫЙ ТРЕНАЖЕР

• Когда n-ное количество клеток в данной области может содержать ровно такое же n-ное количество определенных цифр, эти цифры можно исключить из всех остальных клеток в этой области. Например, в центральном блоке центральная строка может содержать только цифры 3, 5 и 6; следовательно, эти три цифры не могут находиться в остальных двух пустых клетках этого блока.
• Противоположный случай – когда n-ное количество определенных цифр может находиться только в таком же n-ном количестве определенных клеток в данной области. Это позволяет исключить из доступных вариантов в этих клетках все остальные цифры. Например, на рисунке справа показан блок, где только две затемненные клетки могут содержать цифры 1 и 3. Следовательно, все остальные варианты цифр в этих двух клетках можно исключить.

ПОПРОБУЙТЕ СВОИ СИЛЫ









