
Р. Эргашев
Все науки. №2, 2024. Международный научный журнал
Авторы: Алиев Ибратжон Хатамович, Юсупова Анора Каримовна, Xolmatova Nilufarxon Jahongirovna, Кулдашов Голибжон Оббозжонович, Абдурахмонов Султонали Мукарамович, Кулдашов Оббозжон Хокимович, Ibrohimova Adolatxon Adhamjonovna, Рахимова Муштарий Тимуровна, Эргашев Р., Вавилова Екатерина Александровна, G’anieva Sohibaxon, Азамов Валижон
Главный редактор Ибратжон Хатамович Алиев
Редактор Миродилжон Хомуджонович Баратов
Иллюстратор Султонали Мукарамович Абдурахмонов
Иллюстратор Оббозжон Хокимович Кулдашев
Дизайнер обложки Раънохон Мукарамовна Алиева
Научный директор Боходир Хошимович Каримов
Экономический руководитель Ботирали Рустамович Жалолов
Технический директор Султонали Мукарамович Абдурахмонов
Модератор Фарходжон Анваржонович Иброхимов
Корректор Дилноза Орзикуловна Норбоева
© Ибратжон Хатамович Алиев, 2024
© Анора Каримовна Юсупова, 2024
© Nilufarxon Jahongirovna Xolmatova, 2024
© Голибжон Оббозжонович Кулдашов, 2024
© Султонали Мукарамович Абдурахмонов, 2024
© Оббозжон Хокимович Кулдашов, 2024
© Adolatxon Adhamjonovna Ibrohimova, 2024
© Муштарий Тимуровна Рахимова, 2024
© Р. Эргашев, 2024
© Екатерина Александровна Вавилова, 2024
© Sohibaxon G’anieva, 2024
© Валижон Азамов, 2024
© Султонали Мукарамович Абдурахмонов, иллюстрации, 2024
© Оббозжон Хокимович Кулдашев, иллюстрации, 2024
© Раънохон Мукарамовна Алиева, дизайн обложки, 2024
ISBN 978-5-0065-1046-3 (т. 2)
ISBN 978-5-0065-0531-5
Создано в интеллектуальной издательской системе Ridero
ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ
ОТРИЦАТЕЛЬНО-БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ПРИМЕНЕНИЕ В ЖИЗНИ
УДК: 530.1
Юсупова Анора Каримовна
Доктор физико-математических наук, профессор
Ферганский государственный университет, 150100, Республика Узбекистан, Ферганская обл., г. Фергана
Аннотация. В работе приведено основные понятие и общая формула отрицательно-биномиального распределение, продемонстрированы формула коэффициент асимметрии и доказательства распределенном на отрицательно-биномиальном распределении. Приведено сферы, где используется отрицательно-биномиальное распределение и примеры решенные с помощью этого распределения.
Ключевые слова: распределение Паскаля, испытание Бернулли, коэффициент асимметрии, центральный момент третьего порядка, среднеквадратичное отклонение, скошенность.
Abstrackt. The work presents the basic concept and general formula of the negative binomial distribution, demonstrates the formula for the skewness coefficient and evidence of distribution on the negative binomial distribution. The areas where the negative binomial distribution is used and examples solved using this distribution are given.
Key words: Pascal distribution, Bernoulli test, asymmetry coefficient, third-order central moment, standard deviation, skewness.
Annotatsiya. ish manfiy binomial taqsimotning asosiy tushunchasi va umumiy formulasini beradi, assimetriya koeffitsienti formulasini va manfiy binomial taqsimot bo’yicha taqsimotni isbotlaydi. Manfiy binomial taqsimot qo’llaniladigan sohalar va bu taqsimot yordamida hal qilingan misollar keltirilgan
Kalit so’zlar: Paskal taqsimoti, Bernulli testi, assimetriya koeffitsienti, uchinchi tartibli markaziy moment, standart og’ish, egrilik.
Введение
Отрицательное биномиальное распределение, также называемое распределением Паскаля – это распределение дискретной случайной величины, равной числу произошедших неудач в последовательности испытаний Бернулли с вероятностью успеха 𝑝, проводимых до 𝑟-го успеха.
Испытание Бернулли – это эксперимент с двумя возможными исходами – «успех» или «неудача» – и вероятность успеха одинакова при каждом проведении эксперимента.
Примером испытания Бернулли является подбрасывание монеты. Монета может приземлиться только с двух сторон (мы можем назвать орел «успехом», а решку «неудачей»), а вероятность успеха при каждом броске равна 0,5, если предположить, что монета честная. Если случайная величина Х подчиняется отрицательному биномиальному распределению, то вероятность испытать k неудач, прежде чем испытать r успехов, можно найти по следующей формуле:
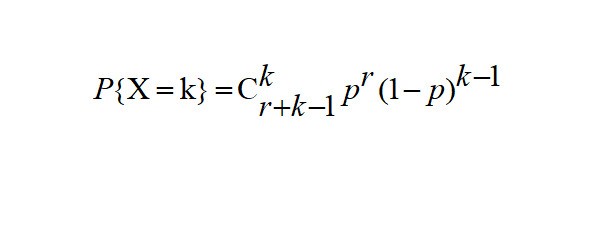
КОЭФФИЦИЕТ АСИММЕТРИИ
Коэффициент асимметрии – это числовая характеристика случайной величины, равная отношению центрального момента третьего порядка к кубу среднеквадратического отклонения.
Коэффициент асимметрии характеризует скошенность распределения по отношению к математическому ожиданию. Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.
Коэффициент асимметрии распределения случайной величины x определяется формулой:
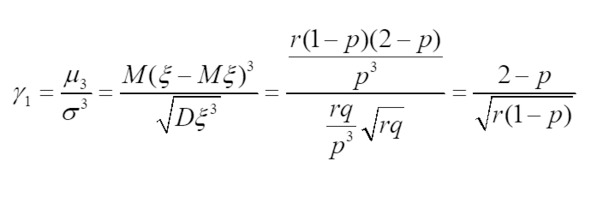
где
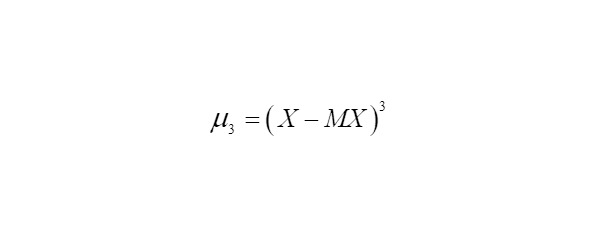
– третий центральный момент случайной величины x;
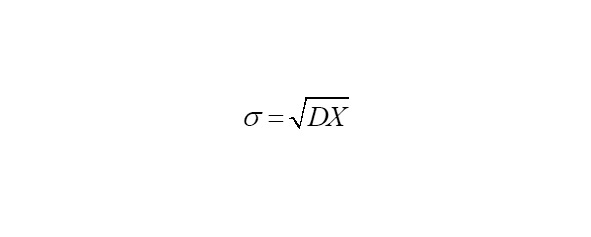
– среднеквадратичное отклонение случайной величины x;

– дисперсия или второй центральный момент случайной величины;
Если плотность распределения симметрична, то
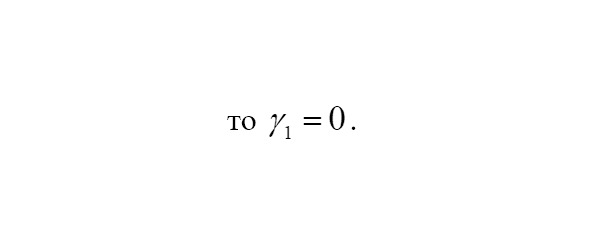
Если левый хвост распределения тяжелее, то

Если правый хвост распределения тяжелее, то
.
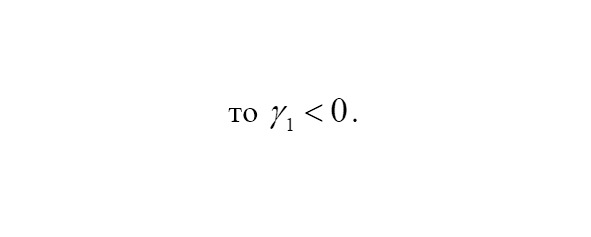

На рисунке показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию, а кривая II – отрицательную (левостороннюю).
Кроме вышеописанного коэффициента, для характеристики асимметрии рассчитывают также показатель асимметрии Пирсона:
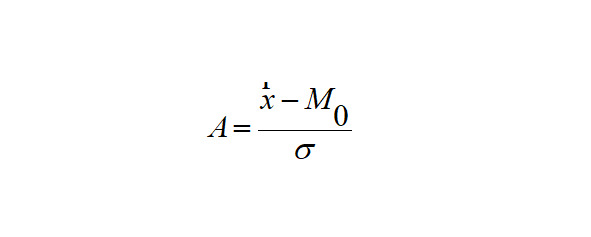
коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента третьего порядка.
ПРИМЕНЕНИЕ ОТРИЦАТЕЛЬНО-БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Отрицательно биномиальное распределение широко используется в различных областях для моделирования случайных событий. Вот несколько примеров использования отрицательно биномиального распределения:
1. Маркетинг и реклама:
Предположим, что компания запускает рекламную кампанию и хочет оценить вероятность того, что клиент кликнет по рекламе до того, как совершит покупку. Отрицательно-биномиальное распределение может быть использовано для моделирования количества кликов до первой успешной покупки.
2. Производство и качество:
В производственной сфере отрицательно биномиальное распределение может быть применено для оценки количества бракованных изделий до достижения определенного числа рабочих изделий. Это помогает предсказать вероятность производственных сбоев.
3.Медицина и здравоохранение:
В медицинских исследованиях отрицательно-биномиальное распределение может использоваться для анализа количества лечебных процедур, которые пациент должен пройти до достижения определенного уровня выздоровления.
4. Финансы и страхование:
В финансовой сфере отрицательно биномиальное распределение может быть применено для прогнозирования количества страховых случаев до возникновения определенного количества убытков.
5. Техническое обслуживание и ремонт:
В сфере технического обслуживания и ремонта отрицательно биномиальное распределение может быть применено для оценки количества обслуживаний или ремонтов, которые требуются до возникновения определенного количества отказов или поломок.
6. Транспорт и логистика:
В логистике и транспортной отрасли отрицательно биномиальное распределение может использоваться для прогнозирования количества перевозок или доставок, которые могут быть выполнены до возникновения определенного числа задержек или неполадок.
7. Образование и наука:
В образовании и научных исследованиях отрицательно биномиальное распределение может быть применено для анализа количества экспериментов или учебных занятий, которые необходимо провести до достижения определенного уровня понимания или результатов.
8. Социология и психология:
В социологических и психологических исследованиях отрицательно биномиальное распределение может использоваться для моделирования количества повторений определенного поведенческого шаблона или реакции до достижения определенного результата.
Отрицательно биномиальное распределение имеет широкий спектр применений в различных областях и может быть полезным инструментом для анализа случайных событий и вероятностей.
Пример 1. Невосстанавливаемая система, работающая циклически, состоит из трех одинаковых по надежности ЭМ: двух основных и одного резервного, автоматически замещающего любой из отказавших основных ЭМ. Вероятность отказа ЭМ на цикле равна q = 0,03. Определить вероятность того, что система проработает 17 безотказно не менее 30-ти циклов, если резервное устройство не нагружено (не включено) и в этом состоянии не отказывает.
Решение.
Как следует из условия задачи, число циклов до отказа системы, равное числу циклов до второго по порядку отказа ЭМ в системе (r = 2) есть случайная величина *n, распределенная по закону Паскаля. Вероятность безотказной работы системы за 30 циклов равна
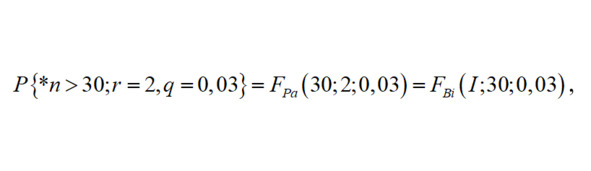
если воспользоваться уравнением связи с Биномиальным распределением. Окончательно из Таблицы при n = 30, q = 0,03 и r = 1, получим

Таким образом, примерно в 77 случаях из 100 такая система проработает безотказно не менее 30 циклов.
Пример 2. Спутник сканирует заданную акваторию океана за 4 оборота вокруг Земли. Если на каком-либо витке из-за различных помех происходит искажение текущего результата, то оно обнаруживается, и сканирование, выполненное на этом витке, повторяется заново. Найти вероятность того, что всё сканирование будет завершено не более чем за 10 витков, если вероятность искажения результата на одном витке составляет 0,2.
Решение
Для решения задачи удобно поменять местами события А – искажение результата сканирования на витке – на противоположное, тогда числу r будет соответствовать число успешно завершенных витков с вероятностью неискажения q = 0,8. С учетом этого замечания и связи с биномиальным распределением искомая вероятность решения задачи не более чем за n = 10 витков запишется в виде:

откуда из Таблицы при r = 6, n = 10 и q = 0,2 получим

то есть примерно в одном случае из тысячи в заданных условиях сканирование не завершится за 10 оборотов спутника вокруг Земли.
Заключение
В работе была сформулирована и доказана формула коэффициент асимметрии распределенном на отрицательно-биномиальным распределении. Была приведено примеры и сферы применение этой распределении.
ИСПОЛЬЗОВАННЫЕ ЛИТЕРАТУРЫ
1. Баврин И. И. Теория вероятностей и математическая статистика / И.И.Баврин. – М.: Высш. шк., 2005. – 160 с:
2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике /В. Е. Гмурман. – М., Высш. шк., 2004.– 404 с.
3. Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика: учебное пособие для вузов /В. Е. Гмурман.-Изд. 12-е, перераб.-М.:Высшая школа,2009.-478с.
4. Гнеденко Б. В. Курс теории вероятностей: Учебник / Б. В. Гнеденко. – Изд. 8-е, испр. и доп. – М.: Едиториал УРСС, 2005. – 448 с.
5. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов / Н. Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2004. – 573 с.
6. Максимов Ю. Д. Вероятностные разделы математики / Ю. Д. Максимов. – Изд.: Иван Федоров, 2001. – 592 с.
АЛГОРИТМ КОМПЛЕКСНОГО АНАЛИЗА РЕЗОНАНСНЫХ ЯДЕРНЫХ РЕАКЦИЙ
УДК: 531.6
Алиев Ибратжон Хатамович
Генеральный директор OOO «Electron Laboratory», Президент Научной школы «Электрон», студент 3 курса факультета математики-информатики Ферганского государственного университета
OOO «ElectronLaboratory», Научная школа «Электрон», город Маргилан, Ферганская область, Республика Узбекистан
Аннотация. В работе рассматривается математический анализ ядерной реакции с бомбардирующими элементарными частицами с высокими и низкими кинетическими энергиями в классическом виде и резонансном состоянии ядерной реакции. В начале приводиться общее уравнение ядерной реакции, после чего осуществляется энергетический анализ с последующим анализом эффективности исследуемой реакции. Следующим этапом анализа реакций является процесс определения эффективности поставленной ядерной реакции с вычислением ядерного эффективного сечения, процента вхождения тока в ядерную реакцию, а также результирующие токи продукта. Теоретическое исследование, в частности, сводилось к моделированию ускорителя заряженных частиц с высокой монохромотичностью, что позволяло анализировать резонансные ядерные реакции. В заключении перечисляются основные выводы, отображающие результаты математического исследования резонансной ядерной реакции.
Ключевые слова: резонансные ядерные реакции, экзо-энергетические ядерные реакции, эндо-энергетические ядерные реакции, Кулоновский барьер, ядерное эффективное сечение.
Abstract. The paper considers the mathematical analysis of a nuclear reaction with bombarding elementary particles with high and low kinetic energies in the classical form and the resonance state of a nuclear reaction. At the beginning, the general equation of a nuclear reaction is given, after which an energy analysis is carried out with subsequent analysis of the efficiency of the reaction under study. The next stage of the reaction analysis is the process of determining the efficiency of the nuclear reaction with the calculation of the nuclear effective cross section, the percentage of current entering the nuclear reaction, as well as the resulting product currents. The theoretical study, in particular, was reduced to modeling a charged particle accelerator with high monochromaticity, which made it possible to analyze resonant nuclear reactions. The conclusion lists the main findings that reflect the results of the mathematical study of the resonant nuclear reaction.
Keywords: resonant nuclear reactions, exo-energetic nuclear reactions, endo-energetic nuclear reactions, Coulomb barrier, nuclear effective cross section.
Annotatsiya. Maqolada klassik shaklda yuqori va past kinetik energiyaga ega elementar zarrachalarni bombardimon qilish bilan yadro reaksiyasining matematik tahlili va yadro reaksiyasining rezonans holati ko‘rib chiqiladi. Boshida yadro reaksiyasining umumiy tenglamasi beriladi, undan so‘ng energiya tahlili o‘tkaziladi, so‘ngra o‘rganilayotgan reaksiyaning samaradorligi tahlil qilinadi. Reaksiya tahlilining navbatdagi bosqichi – yadro effektli kesimini, yadro reaksiyasiga kiradigan tokning foizini, shuningdek, hosil bo’lgan mahsulot oqimlarini hisoblash bilan berilgan yadro reaktsiyasining samaradorligini aniqlash jarayoni. Nazariy tadqiqot, xususan, yuqori monoxromatiklik bilan zaryadlangan zarracha tezlatgichini modellashtirishga qisqartirildi, bu rezonansli yadro reaktsiyalarini tahlil qilish imkonini berdi. Xulosa qilib, rezonansli yadro reaktsiyasini matematik o’rganish natijalarini aks ettiruvchi asosiy xulosalar keltirilgan.
Tayanch iboralar: rezonansli yadro reaksiyalari, ekzoenergetik yadro reaksiyalari, endoenergetik yadro reaksiyalari, Kulon to’sig’i, yadro effektli kesma.
Введение
Как известно, в ядерной физике и физике элементарных частиц теоретически и экспериментально изучены ядерные реакции, образованные под воздействием бомбардировки заряженных частиц с различными кинетическими энергиями []. Но в этих исследованиях сами процессы изучены раздельно. В этих работах, изучен процесс бомбардировки ядер-мишеней мало энергетическими и высокоэнергетическими заряженными частицами, на различных типах ускорителей – от линейных ускорителей и циклотронов до синхрофазотронов. В проведённых исследовательских работах основное внимание направлено на экспериментальный аспект исследования, а теоретический анализ достаточно не проведён. Поэтому проведение исследований ядерных реакций бомбардировки заряженных частиц с различными кинетическими энергиями с выводом их эффективности является актуальным.
Важно при этом отметить, что до настоящего времени не было единой комплексной модели анализа ядерных реакций, которая к тому же позволила определить новый тип ядерных реакций – резонансные ядерные реакции, кроме существующих классических реакций экзо-энергетического и эндо-энергетического типа, термоядерных реакций и реакций распада. Откуда видна необходимость математически определить резонансное состояние ядерных реакций на типе ускорителей с высокой монохромотичностью.
Материалы и методы
Для исследования вышеуказанных процессов подобраны различные теоретические подходы анализа и решения многомерных физико-математических выражений. Объектов исследования являлись ядерные реакции, проходящие после бомбардировки заряженными частицами ядер-мишеней с высокими, низкими кинетическими энергиями в классическом виде, в резонансном состоянии.
ИССЛЕДОВАНИЕ
Вначале можно рассмотреть некоторые виды ядерных реакций: реакции с одним ядром и направленной частицей, либо с двумя направленными частицами. Каждая из этих реакций в свою очередь подразделяются на экзо-энергетические, то есть реакции с положительным выходом реакции и эндо-энергетические, то есть с отрицательным выходом реакции. Также существуют реакции распада для тяжёлых ядер. Стоит также условиться, что каждая из этих реакций рассматриваются в масштабах атомных ядер, поскольку для более малых элементарных частиц или более масштабных атомных и молекулярных мерах имеют место прочие специальные типы реакций с линиями взаимодействий между каждыми из составляющих реакции.
Однако, на практике чаще всего встречается реакции столкновения на неподвижную мишень направленных частиц, что и приводило к большому числу результатов, однако, имеют место случаи, когда результатом такого столкновения становились ядра, в свою очередь распадающиеся на составные части. Либо, подобный результат наблюдался и при коллайдерном столкновении, то есть, когда один пучок становился мишенью относительно второго и второй становился мишенью относительно первого. Этот фактор привёл к тому, что эти реакции с бомбардировкой частиц также кроме экзо-энергетического и эндо-энергетического типа подразделились на мгновенные и на составные. Всё дело в том, что это определяется уже из энергии направленных частиц и если она сравнительна велика для той или иной реакции, наряду с прочими составляющими моментами, откуда определяется время прохождения самой реакции, то она может пройти мгновенно, образовав продукты реакции, тогда направленные частицы буквально выбивают из составного ядра части продуктов ядерной реакции.
Для составных реакций существует алгоритм, по которому мишень сливается на определённое время с направленной частицей, после чего уже начинает распадаться, начав новое образование без учёта предыдущих импульсов. В таком случае в одной только реакции направленных частиц включается и реакция распада, откуда можно сделать вывод о неразрывной связанности этих двух типов ядерных реакций. Но теперь стоит переходить к полному анализу определённо заданной реакции, с соответствующими условиями, а именно, самой реакцией (1), её основного канала, массами всех составляющих этой реакции – Ma, MA, MB, Mb и кинетическую энергию направленной частицы Eka1 до проведения ядерной реакции и барьера ядра.

Первоначально, цель такого анализа – определить все необходимые аспекты и свойства заданной ядерной реакции. При этом необходимо учесть, что реакция ещё не началась и нужно сначала определить кулоновский барьер (2) частицы-мишени, на которую направлена частица-заряд

Стоит сказать, что чаще всего в формуле (2) используются две константы, заменяющие элементарный заряд, это постоянная тонкой структуры, равная 1/137 и произведение приведённой постоянной планка, умноженная на скорость света, измеряемая в МэВ равная 197,3 МэВ. Эти единицы сводятся к тому, что справедливо равенство (3) и явно упрощение всего выражения.
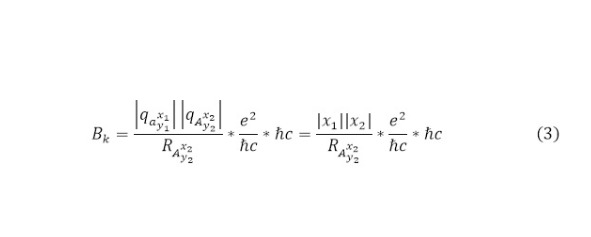
Радиус ядра может быть выбран в качестве крнстанты, но чаще всего използуеться соотношение (4).

Выражение (4) вычисляется в ферми, равная фемтометру или 10—15 м.
Ныне же, когда была определена кинетическая энергия и кулоновский барьер, а также частица уже прошла через него, затратив определённую часть своей энергии и вошла в реакцию, преодолев расстояние в 10—15 от ядра – радиус кулоновского барьера, можно определить значение новой кинетической энергии (5), указывая некоторое примечание того, что первоначальная здесь указанная кинетическая энергия определена после прохождения частицы через атомную структуру того или иного материала, в состав которой и входит ядро-мишень, однако подобный алгоритм чаще всего относится к атомному, молекулярному масштабу и траты на эти явления не столь существенны, чаще всего представляясь в форме некого рассеяния на настоящем материале.
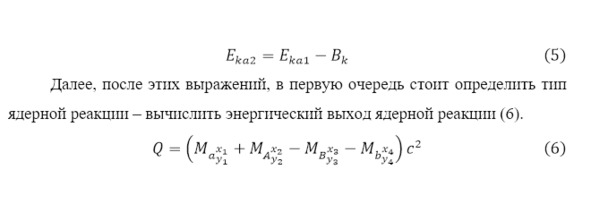
Более простое вычисление настоящего выражения может быть обеспечено за счёт того, что масса каждой из составляющих ядерной реакции вычисляется в атомных единицах массы и после проведения элементарных арифметических действий умножается на квадрат скорости света, также представленный в МэВ, которая для 1 а. е. м. равняется 931,5 МэВ. В результате получается положительный или отрицательный выход ядерной реакции, откуда можно определить экзо- или эндо-энергичность ядерной реакции.
Выше утверждалось, что частица может затрачивать определённую энергию, которая будет тратиться не только на кулоновский, но и прочие другие барьеры. Для того, чтобы определить их некоторую приближенную
сумму, используется понятие энергетического порога ядерных реакций (7).

В данном случае все необходимые показатели известны и дают общее состояние реакции. Далее, желательно представлять общее энергетическое уравнение такой ядерной реакции (8), после чего можно переходить к определению кинетической энергии результатов ядерной реакции.
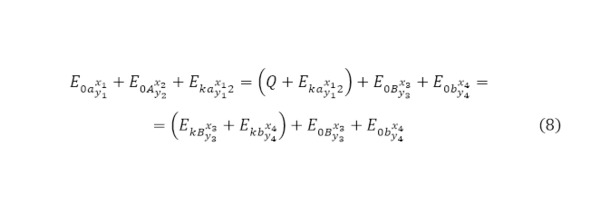
Для того же, чтобы определить кинетическую энергию продуктов ядерной реакции необходимо отметить, что каждая из частиц получает изначальный энергетический дополнительный баланс, равный сумме выхода реакции и второй кинетической энергии направленной частицы после кулоновского барьера, в обратно-пропорциональном собственной массе соотношении (9—10).

Более выраженным становиться представление этих выражений уже для трёх продуктов реакции. Чаще всего в таком случае получается момент, когда частицы разделяются на две группы – лёгкие и тяжелые группы. Лёгкая группа получает по вышеуказанным причинам большую часть от общей энергии и такой алгоритм сохраняется в соответствующим образом.
Так, если количество выходящий частиц будет стремиться к определённому большому числу (11), то их энергии будут распределяется соответствующим обратно-пропорциональным, их массе, образом (12), учитывая выход реакции (13) для такого (11).

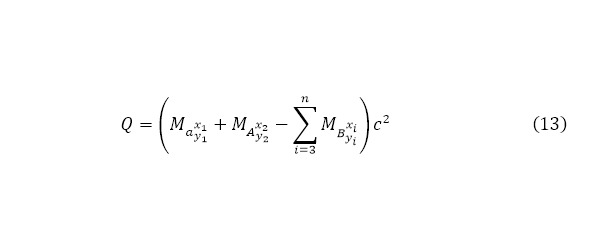
После того как определяется кинетическая энергия каждой из результатов реакции, становиться необходимым определить такое понятие как ядерное эффективное сечение ядерной реакции (14).
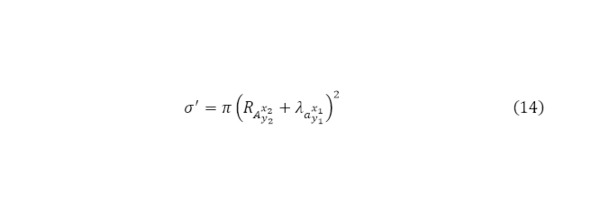
Это понятие находит своё начало в квантовой физике, согласно законам которого даже если частица не попала в физическую корпускулярную площадь ядра, то оно может быть им захвачено в следствие своей малой скорости, за счёт чего растёт волна де Бройля направленного пучка (15).
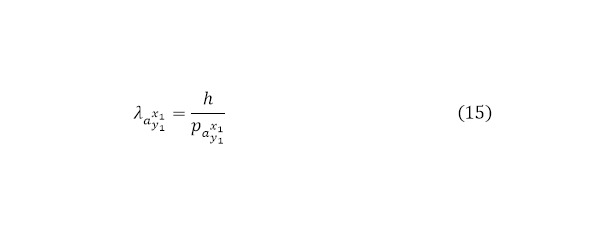
Для вычисления импульса направленной частицы при этом, согласно теории относительности используется (16), учитывая тот факт, что ядерное эффективное сечение, как и все следующие за ней функции определяются во временном масштабе после преодоления пучком кулоновского барьера, откуда и импульс, и скорости берутся непосредственно вторые, учитывая тот фактор, что за счёт увеличения ядерного эффективного сечения, кратковременно ядерные силы вместе кулоновским барьером увеличиваются в размерах.

Где скорость направленной частицы из кинетической энергии вычисляется благодаря выводу через (17).

В результате проведённых вычислений удалось определить ядерное эффективное сечение, которое изменяется в квадратных метрах, однако для него введена специальная единица – барн, равная 10—28 м2 []. Но стоит указать некоторую особенность в том определении, что значение (14) является приведённым ядерным эффективным сечением, которое для практического значения переводиться через (19), где применяется константа (18), являющаяся безразмерной величиной, которая выражается через отношение практического экспериментально определённого значения ядерного эффективного сечения чаще всего используемой ядерной реакции – реакции распада урана равная 584 барна к теоретической основе, равная 3 396 747,21529 барн.

Далее, когда определено это значение, оно нужно для того, чтобы определить какая часть из всех направленных частиц действительно пройдёт через ядерную реакцию и сможет дать результат, для этого используется следующий алгоритм. Пусть на мишень налетает N (x) частиц, а после преодоления мишени, количество частиц составляет N (x) -dN, откуда dN – число всех произошедших в мишени взаимодействий. Теперь, определим, что координата на начале мишени – x, а на моменте выхода – x+dx, следовательно dx – толщина мишени. Затем вводиться определение понятия плотности ядер мишени, для того чтобы его вычислить необходимо воспользоваться (20).
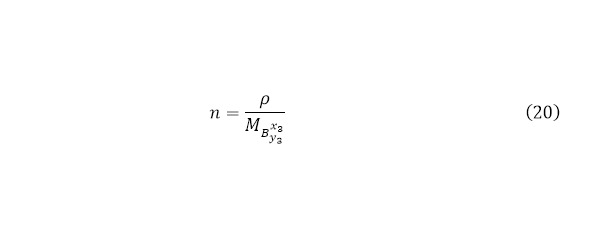
Это количество ядер, присутствующие в одном кубометре используемого вещества, следовательно, исходя из введённых определить и обозначений, можно прийти к выводу, что во всей мишени имеется (21) ядер, а если учитывать, что площадь куда попадая частицы входят во взаимодействие, считая как площадь единичного случая, куда достаточно попасть одной направленной частице, чтобы реакция произошла, принять (14), то для всей мишени это значения может быть определено согласно (22).

Теперь можно определить отношение всей площади, попадая на которое можно вызвать начало реакции ко всей площади мишени, которое будет равняться отношению частиц, которые вошли в реакцию ко всем частицам – функции, выражающая в начальный момент времени это значение, направленные в пучке изначально (23).

Получая такое выражение, можно проинтегрировать обе части, указав, что количество частиц, как известно – функция, которая по определённому интегралу будет брать в себе границы от изначального количества направленных частиц к количеству взаимодействий в мишени для первого интеграла. Для второй же стороны этот определённый интеграл имеет границы от нуля до значения крайней толщины мишени (24—25) [].
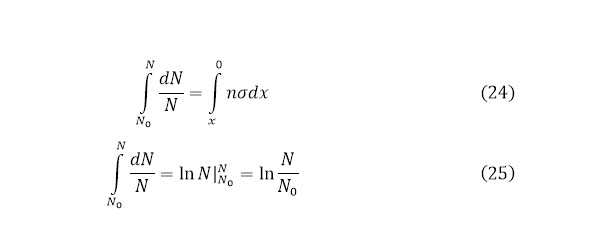
Для второго интеграла границы меняются, как и знак выражения (26) с дальнейшим преобразованием (27).

Из этого соотношения можно получить уравнение, которое бы описывало количество частиц входящих во взаимодействие (28) и откуда можно было бы вычислить процентную эффективность ядерной реакции (29).

Таким образом, можно говорить о том, что ядерная реакция прошла в количестве (28) с общей процентной эффективностью (29) с кинетической энергией для вылетающих лёгких частиц (10) и общим зарядом вылетающих частиц (30) и получаемым в результате током (31), соответствующей площадью вылетающей мишени (32), наряду со всеми учитываемыми скоростями вылетающих частиц (33).
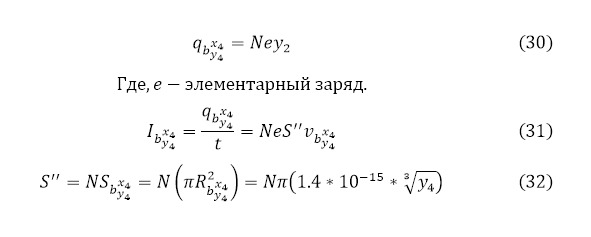

Кроме того, из (29) можно вывести и время ядерной реакции (34).
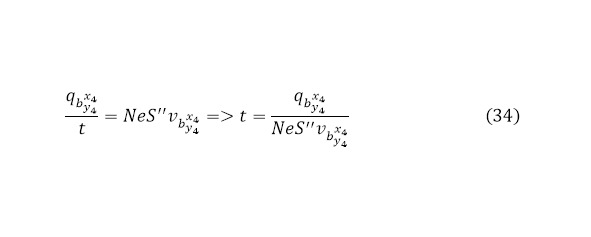
Но здесь были рассмотрены только лёгкие продукты реакции, которые в общей сумме дают мощность, определяемая через (35), как и выполняемая работа (36), а относительно тяжёлых ядер – их энергии не будет достаточной для ускорения, из-за чего она преобразуется в тепловую энергию (37) за счёт малых образуемых скоростей тяжёлых ядер (38).

Однако эта кинетическая энергия быстро распределяется по всему материалу, поэтому определённая в (37) температура относиться только к части образованных новых ядер, а для вычисления температуры мишени после реакции (39) достаточно распределить общую энергию полученных ядер на весь материал.
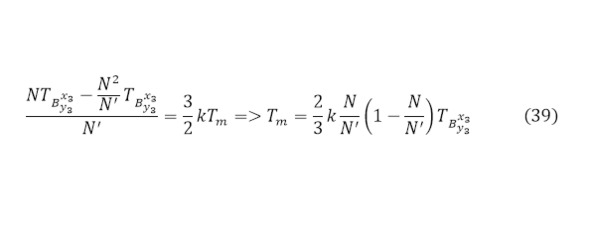
Таким образом были получены вылетающие частицы с определёнными параметрами и ядра с определёнными температурами. Однако есть такое понятие как выходящий кулоновский барьер. Величина, определённая в (3) является именно входящим кулоновским барьером, а для выходящего кулоновского барьера это выражение преобразуется как (40) с радиусом образуемого тяжёлого ядра, вычисляемый через (41).
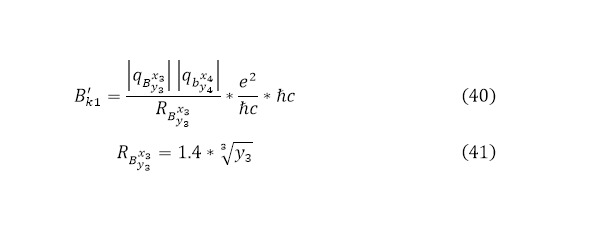
К тому же интересным является случай, когда количество частиц больше двух (11), тогда необходимо обратиться к сумме, где кулоновский выходящий барьер начинает суммироваться для одной частицы, получающая энергию от всех остальных частиц и одноимённым с ней зарядом (42—47) и здесь не учитываются соотношения с прочими частицами в пучке, поскольку это явление действует на рассеяние пучка, когда же здесь учитываются масштабы именно после ядерной реакции с близкими расстояниями.
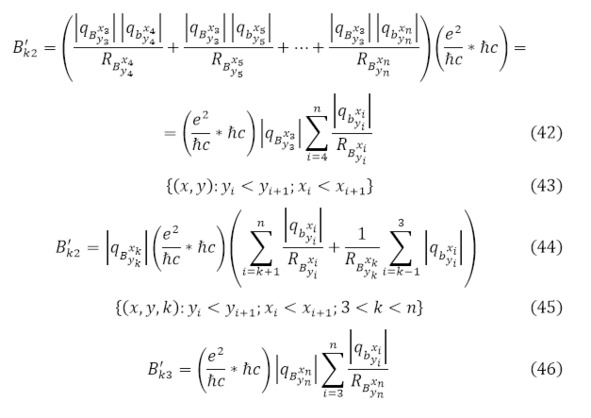
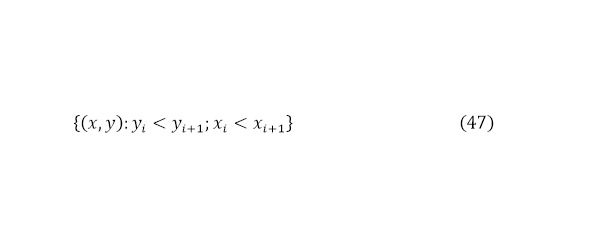
Где (42) используется для самой лёгкой частицы из всех полученных продуктов реакции в множестве (43); для всех промежуточных продуктов реакции (44) на множестве (45) с его условиями; для самой тяжёлой частицы (3.46) в масштабах множества (47).
По определению величина выходящего кулоновского барьера, как можно увидеть, описывается как энергия, которую приобретают вылетающие частицы, отталкиваясь друг от друга, сразу после преодоления ядерных сил и до убывания с ростом расстояния между ними и поэтому каждая из частиц получают эту энергию, за счёт чего, если формулы кинетических энергий лёгких продуктов реакции практически не меняются, то для тяжёлых частиц формулы (37—39) приобретают новую форму в (48—50).

Но прежде, чем продолжить анализ, стоит рассмотреть случай, когда образованное ядро может быть радиоактивным.
В таком случае стоит проанализировать реакцию вида (51).
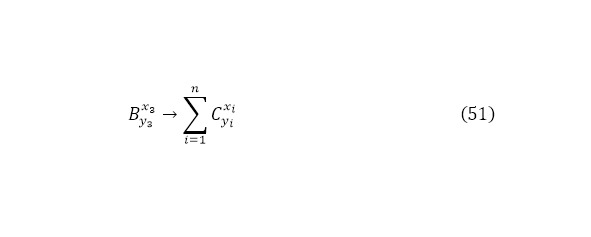
Ровно как проводился анализ для реакции (1), для реакции (51) проводиться подобный алгоритм, но, разумеется, не определяется кулоновский барьер, поскольку нет для этой реакции направленной частицы, поэтому определяется выход этой реакции (52), а затем и кинетическая энергия для всех продуктов реакции (53).
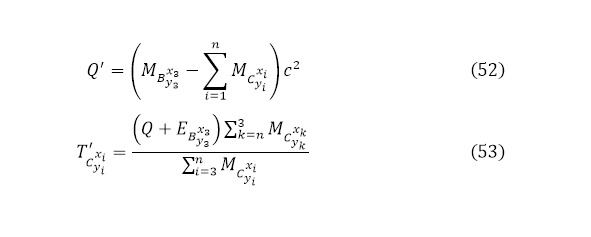
И одним из заключительных моментов анализа реакции распада является указание закона ядерного распада (54).
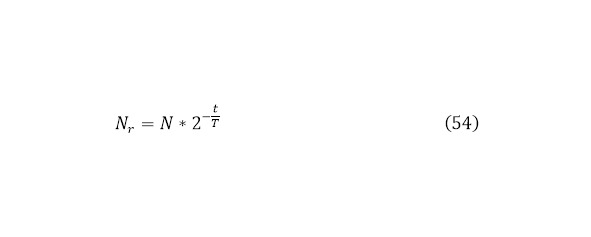
В данном случае, получается определённое стабильное ядро и лёгкие частицы, с определённой кинетической энергией и известной скоростью (55).

Если же настоящее ядро будет вновь радиоактивным, хотя подобные случае довольно редки, но для них действует тот же алгоритм анализа реакций распада. В данном случае также каждая из частиц будет отталкиваться, получая дополнительный выходящий кулоновский барьер, что и учитывается.
В данном случае для ядра кинетическая энергия и образуемая с его стороны температура объясняется посредством уже выведенных закономерностей для образованной части (56) и для всей мишени (57), а для лёгких частиц известна кинетическая энергия, а также заряд через (58) и ток (59).

Однако, на этом не завершается анализ реакции, поскольку ныне проанализирован только один канал ядерной реакции, откуда следует, что стоит обратить отдельное внимание на все возможные различные комбинации (60).







