Ингве Фогт
Математические трюки для быстрого счёта

Полная версия

2
Проще некуда
Семь правил, которые вам понадобятся

Дорогой читатель, позвольте вас успокоить. Чтобы учиться быстрому счету по этой книге, никаких особых познаний в математике вам не понадобится. Единственное, что от вас потребуется, – это помнить несколько простейших базовых правил, которым учат еще в начальной школе. И больше ничего, обещаю! Честное слово, даже если вы не станете читать эту главу, тех правил достаточно, чтобы вы справился с остальными главами моей книги.

Итак, в основе книги лежат семь легких математических правил. Сравнить их можно с содержимым столярного ящика. Строя прекраснейшие дома, плотник пользуется лишь пилой и топором. Вот и вам понадобится всего несколько математических инструментов, чтобы стать мастером быстрого счета. Некоторые из этих инструментов такие простые, что вы, возможно, сочтете лишним их упоминать. Но я все равно расскажу о них – во-первых, потому что они важные, а во-вторых, потому что они простые и лишний раз порадуют вас.

Правило 1

Первое правило на удивление простое. Порядок чисел при умножении роли не играет:

a × b = b × a

Если буквы вам не по душе, могу продемонстрировать то же самое на простейшем цифровом примере.

3 × 7 даст тот же результат, что 7 × 3. Итак, то, в каком порядке перемножать числа, совершенно не важно.

Правило 2

Второе правило тоже манна небесная для тех, кто пребывает в заблуждении и считает математику сложной.

Порядок чисел при сложении роли не играет.

a + b = b + a

И вот вам пример: 2 + 3 дадут в результате то же число, что и 3 + 2.

Правило 3

Квадрат определенного числа выглядит следующим образом: a × a = a².

Обратите внимание на крошечную цифру 2 над последней «а» – читая эту книгу, вы успеете близко с ней познакомиться. Математики называют такие цифры степенями.

Вот еще пример: 3 × 3 можно обозначить как 3².

Разумеется, отрицательные числа тоже можно возводить в квадрат:

(‒a) × (‒a) = (‒a)² = a²

Например: (‒3) × (‒3) соответствует (‒3)².

А вот это невероятно красиво:

(‒3)² дает тот же результат, что и 3².

Правило 4

На квадратные корни тоже приятно посмотреть:

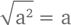
Это означает, что если извлечь квадратный корень из возведенного в квадрат числа, то это же число и получится.

На языке цифр это выглядит вот так:

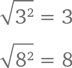
Правило 5

Когда надо умножать отрицательные числа, многие впадают в ступор. Если вас это тоже касается, то быстрому счету вам придется учиться долго.

Одно из важнейших правил звучит так: минус на минус дает плюс.

(‒x) × (‒y) = x × y

Примеры:

(‒2) × (‒3) = 2 × 3 = 6

(‒4) × (‒5) = 4 × 5 = 20

А вот если минус умножить на плюс, то получится, наоборот, минус:

(‒x) × y = ‒(x × y)

Примеры:

(‒2) × 3 = ‒(2 × 3) = ‒6

4 × (‒5) = ‒(4 × 5) = ‒20

Запомним это – минус на минус и минус на плюс, и тогда все минусы математики превратятся для вас в плюсы!

Правило 6

Если хотите понять доказательства приведенных в этой книге методов, придется научиться разлагать числовые выражения на множители и раскрывать скобки:

a(b + c) = ab + ac

(a + c)(b + d) = ab + ad + cb + cd

Вот и все – больше про разложение на множители знать нам ничего не понадобится.

Правило 7

Некоторые методы быстрого счета в этой книге основаны на трех видах квадратичных тождеств, которые включены в стандартную школьную программу. Все они – особые случаи правила 6:

(a + c)(b + d) = ab + ad + cb + cd

Квадратичное тождество первого типа:

(a + b)² = a² + 2ab + b²

Квадратичное тождество второго типа:

(a ‒ b)² = a² ‒ 2ab + b²

Квадратичное тождество третьего типа:

(a + b)(a ‒ b) = a² ‒ b²

С этими семью правилами в готовальне у вас есть все шансы стать чемпионами быстрого счета. Ну что ж, пора отправляться завоевывать мир! Удачи и успехов!

3
Ходячий калькулятор
Чемпион мира по быстрому счету

В начальной школе я терпеть не мог спорт, зато мечтал стать чемпионом мира по решению в уме всяких математических примеров. Поэтому мне казалось ужасно несправедливым, что школьные спортсмены то и дело выступали на разных соревнованиях, ведь соревнований по математике просто не существовало. Сейчас-то я понимаю, что мое мнение о собственных математических способностях было необоснованно завышенным, я жил в мечтах: хотя считал я и правда довольно быстро, а числа так просто обожал, моих способностей не хватало, если числа в примерах были больше приведенных в таблице умножения. Впрочем, об этом никто не догадывался. Слухи о моих феноменальных математических способностях разлетались со скоростью света и с действительностью ничего общего не имели. Никогда не забуду, как мама одного из моих одноклассников на глазах у всего класса погладила меня по голове и выразила свое восхищение: еще бы, ведь я умею в уме перемножать многозначные числа. Мне тогда было девять лет. А еще мама моего одноклассника слышала, будто я умею и миллионы перемножать. Все это было неправдой, но стеснительность помешала мне опровергнуть слухи. Я смотрел на эту женщину и вспоминал, как однажды, будучи первоклашкой, возвращался из школы домой и был пойман шестиклассниками, которые потребовали сделать за них домашку по математике. Они крепко держали меня (впрочем, особых усилий от них не требовалось – я был самым мелким во всей школе) и, пока я не решил все задачки, не отпускали.

Задачки у них оказались очень простыми. В одной я нарочно допустил ошибку – хотел проверить, заметят ли они, но они, к моей великой радости, ничего не заподозрили. Легенда о моем таланте вдребезги разлетелась в шестом классе, когда отец отвел меня к университетскому профессору, предварительно рассказав ему о моих невероятных успехах. Профессор дал мне несколько примеров и выглядел довольно-таки разочарованным, когда я ошибся в первом же из них. Именно в тот момент я понял, что лучше всего считаю в спокойной обстановке и наилучшее впечатление произвожу на тех, кто сам с математикой не дружит.

В уме быстрее всех в мире считает американец по имени Скотт Фленсбург, и для него обстановка никакого значения не имеет. Его часто приглашают на знаменитые ток-шоу, а звезда американских телеэкранов Реджис Филбин назвал Фленсбурга живым калькулятором. Скотт Фленсбург посчитает в голове быстрее, чем мы успеем посчитать на калькуляторе. 27 апреля 2000 г. он попал в Книгу рекордов Гиннесса, потому что за 15 секунд наибольшее количество раз прибавил случайно выбранное двузначное число. Ему досталось число 38, и за это ничтожно короткое время он успел прибавить его 36 раз и выдать ответы: 38, 76, 114, 152, 190, 228 и так далее до 1368. Это означает, что одной секунды ему хватало, чтобы прибавить число 38 два раза. Мягко говоря, потрясающе. Попробуйте сами! Так быстро считать еще никому не удавалось!

Как сказал, демонстрируя по телевизору свой рекорд, он сам, «встроенный в мозг калькулятор – это щедрый подарок, вот только слова мешают». Дело в том, что считает Фленсбург быстрее, чем успевает произнести ответ, хотя говорит тоже не медленно. Это несоответствие скорости работы мозга темпу речи можно сравнить с супербыстрым компьютером, подключенным к постоянно зависающему принтеру.

С такой же скоростью Скотт Фленсбург умножает и делит числа. Мы еще и калькулятор не успеем включить, а он уже извлечет квадратный и кубический корень и с той же скоростью выдаст ответ, даже если в нем имеются дроби. «Я не атлет, я матлет», – повторяет он словно мантру. Если имена великих спортсменов – Златана, Роналду и Болта – знакомы каждому, то матлеты не известны никому. А ведь как чудесно было бы узнать о них в детстве!

Фленсбург утверждает, что в голову каждого из нас встроен калькулятор. Он размером с виноградину, и его можно натренировать. Чем он больше, тем лучше ты считаешь. Вот только в нашем обществе быть плохим математиком не предосудительно, и поэтому Фленсбург решил посвятить свою жизнь тем, кто любит числа, и помочь тем, кто не питает к числам особенно теплых чувств, понять, насколько занятная штука счет. Приезжая в школы в самых разных уголках мира, Скотт Фленсбург просит учеников придумывать для него примеры. Школьники при этом уже держат наготове калькуляторы. Они еще и кнопки нажать не успевают, когда у матлета, к бесконечному восторгу зрителей, уже готов ответ. «Калькулятор начинает с нуля. И мой мозг тоже. Я всегда начинаю с нуля и забываю о прошлом и будущем». Фленсбург обнаружил свой калькулятор совершенно случайно и благодарит за это своего потрясающего школьного учителя математики. В девятилетнем возрасте он придумал способ складывать числа быстрее, чем учитель, – Фленсбург складывал числа в любом порядке, и получалось у него это невероятно быстро. Именно тогда он и понял, что представляет собой своеобразный человеческий калькулятор. С тех пор этот метод стал его коньком. Сами представьте: вам надо сложить четыре двузначных числа – 13, 14, 16 и 17. Большинство из нас начнут с того, что сперва сложат единицы, а следом – десятки. По мнению Скотта Фленсбурга, это наихудший метод, потому что ответ можно прикинуть не сразу. «Это же совершенно нелогично. Ведь читать-то мы учимся слева направо, однако математические примеры нас учат решать справа налево. На самом деле следовало бы и считать тоже слева направо». Его совет таков: первым делом складывайте десятки, и тогда вы сразу же узнаете примерную итоговую сумму.

Одна из самых интересных математических игр, в которую Фленсбург играет со школьниками во время своих многочисленных турне, – привести любой пример к числу 9. Возьмем любое случайное число, например 28, сложим составляющие его цифры и вычтем их сумму из самого числа: 2 + 8 = 10 и 28 ‒ 10 = 18. Проделаем то же самое с получившимся числом: 18 ‒ (1 + 8) = 9. Не важно, с какого числа начинать и большое ли оно – в итоге все равно получится 9.

Скотт Фленсбург не только придумывает математические игры для школьников – он также помогает студентам и их родителям преодолеть страх перед математикой. Скотт уверен: возможность хорошо считать и завести у себя в голове собственный калькулятор есть у каждого. В 2014 г. этот математический гений в четвертый раз посетил Норвегию, где выступил перед 20 000 учеников и учителей. Его цель – встретиться со всеми девятилетками в мире и объяснить им, что математика – это не зубрежка, а часть нашего естественного человеческого языка. Как он сам пишет в книге «Волшебство математики» (Math Magic), «мир вокруг нас полон чисел. Тот, кто не понимает числа, ограничен так же, как и тот, кто не умеет читать». Скотт Фленсбург старается развеять миф о том, что математика доступна только ученым. Он полагает, что некоторые техники быстрого счета способны изменить наше понимание чисел, так что страх перед числами сменится восхищением. Хотя сейчас Фленсбург считает быстрее всех в мире, техники быстрого счета разрабатываются уже на протяжении нескольких тысячелетий. В следующей главе я расскажу о том, как люди в разные эпохи записывали числа (а порой эти способы очень отличаются от современных) и использовали их в вычислениях. Это намного интереснее детективных романов, поэтому быстрее перелистывайте страницу и переходите к следующей главе.