
Ник Антилл
Оценка компаний: Анализ и прогнозирование с использованием отчетности по МСФО
3. Денежные статьи баланса, начисления и прибыль
Представьте себе компанию – владельца недвижимости, которая ежегодно имеет доход от аренды в размере 5 % от рыночной стоимости своей собственности. Кроме того, рыночная стоимость имеющейся собственности компании растет на 5 % в год. Ее административные и финансовые затраты также составляют ежегодно 5 % рыночной стоимости ее портфеля.
Это достаточно простая компания. У нее нулевой денежный поток до новых инвестиций в новые объекты собственности, но если компания начинает расширяться, ее денежный поток оказывается отрицательным. Ее стоимость растет каждый год в результате новых инвестиций и 5 %-ного роста стоимости первоначального портфеля.
Теперь представим, что мы рассчитываем дисконтированный денежный поток нашей компании. Пока она росла, то должна была иметь отрицательный денежный поток. При прекращении роста денежный поток окажется нулевым. Но стоимость портфеля компании при этом продолжала бы расти на 5 % в год без новых инвестиций. В любой момент можно было бы обратить эти начисления в наличность – просто надо ликвидировать портфель и реализовать ценности. Мы хотим разработать метод оценки, который отражал бы, что компания добавила 5 % к стоимости своих первоначальных активов, но не учитывал этот факт в ее денежном потоке.
Мы выявляем две формы прироста стоимости нашей компании. Первая – реальный денежный поток, создаваемый рентными платежами. Вторая – увеличение стоимости объектов собственности без их реализации. Им противопоставляются управленческие и финансовые затраты.
Рассмотрим другой пример. Предположим, что мы анализируем энергетическую компанию, все предприятия которой – атомные электростанции. Можно ожидать, что они почти постоянно будут генерировать существенные денежные потоки, поскольку текущие затраты атомной электростанции малы. Однако расходы на предстоящий вывод станции из эксплуатации достаточно велики. Поэтому данная генерирующая компания может отражать в финансовой отчетности прибыль за вычетом значительных резервов на возможную консервацию атомной станции.
Здесь ситуация, противоположная первому случаю. Дисконтирование растущих бесконечно совокупных денежных потоков на основе отчетности этой компании даст неправдоподобно высокую ее оценку, поскольку при этом неявно предполагается, что ее атомные станции будут существовать вечно. Можно ли решить проблему, принимая резервы, включенные в бухгалтерский баланс и вычитая их из нашей оценки, как если бы они были заимствованиями? Нет, поскольку так можно поступать только с затратами, которые связаны с ликвидацией этого поколения атомных станций. А как быть с генераторами нового поколения? Помимо всего прочего, мы экстраполируем объем продаж в бесконечность, но тогда мы должны экстраполировать в бесконечность и эти огромные, крайне нерегулярные затраты.
Все это вынуждает создавать весьма странные на вид модели дисконтированного денежного потока. В некоторых случаях мы обнаруживаем, что при определении понятия «денежный поток» вынуждены включать в него неденежные показатели (например, упущенная выгода). В других случаях мы вынуждены вычитать из наших денежных потоков неденежные статьи (например, зарезервированные средства, которые представляют собой реальные затраты для компании).
Замечание. Оценку компаний можно проводить, используя анализ дисконтированных денежных потоков (DCF) при условии, что эти потоки построены с учетом поправок. При этом мы исключаем из денежных потоков часть, которая нам не принадлежит, и добавляем начисленный доход, который еще не получен, но может быть получен.
4. Модель расчета экономической прибыли
Сейчас самый подходящий момент представить альтернативу DCF: модель экономической прибыли. Эта модель может применяться при оценке акционерного капитала (остаточный доход) и при оценке капитала (модель добавленной экономической стоимости EVATM).
Модель экономической прибыли исходит из того, что стоимость – это балансовый показатель (затраты на приобретение актива) плюс или минус поправка на разницу между фактической и ожидаемой доходностью. (Ниже мы покажем, что и модель дисконтированных денежных потоков, и модель экономической прибыли дают одинаковый результат как для компании с постоянным темпом роста, финансируемой только за счет собственного капитала, так и для более приближенной к действительности компании.) Привлекательность модели, основанной на экономической прибыли, состоит в том, что используются балансовые показатели, следовательно, используются начисленные значения, которые влияют на оценку компании. Если оценка значительно изменяется при использовании прибыли, очищенной, например, от затрат на ликвидацию предприятия в будущем, то оценщик обязательно скорректирует вычисления. В модели дисконтированных денежных потоков такое изменение не заложено. Как мы увидим в последующих главах, это означает, что мы часто хотим учесть одни изменения инвестированного капитала и исключить другие. Поэтому, независимо от метода оценки, надо очень внимательно анализировать составляющие свободного денежного потока и прибыли.
Теперь применим модель Гордона к акционерному капиталу. Как и прежде,
V = D / (k – g),
D = B × R × (1 – b)
где B – балансовая стоимость (акционерного капитала), R – доходность собственного (акционерного) капитала и b – коэффициент удержания. Таким образом, модель Гордона может быть переписана следующим образом:
V = B × R × (1 – b) / (k – g).
Поскольку g = b × R,
V = B × (R – g) / (k – g).
В табл. 1.5 показана зависимость коэффициента «цена / балансовая стоимость капитала компании» от изменения темпов роста и доходности собственного (акционерного) капитала. Эта таблица похожа на приведенную выше таблицу, значения которой рассчитывались с использованием данных о доходе. Аналогичные комментарии, естественно, применимы к соотношению прибыльности, роста и стоимости. Почему ответы одинаковы только для строки, в которой доходность на собственный (акционерный) капитал равна 10 %? В соответствии с табл. 1.3, на 1000 ед. инвестированного капитала с доходностью 10 % мы получили 100 ед. прибыли, но мы не учитывали ожидаемую доходность нового капитала. Теперь же мы предположили, что новый и старый капитал приносят одинаковую доходность. Различие имеет решающее значение (хотя часто игнорируется в оценочных моделях), и мы вернемся к нему в главе 3.
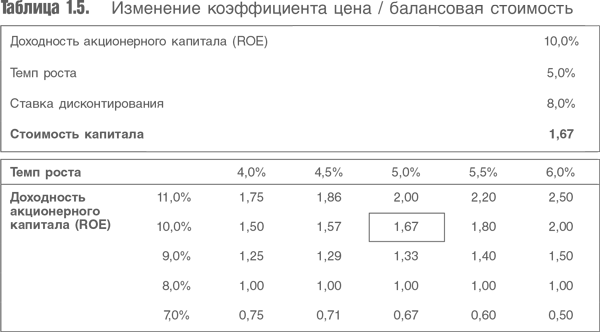
Чтобы лучше понять суть данного метода, нужно приравнять темп роста к нулю. В этом случае отношение стоимости к балансовой стоимости становится равным отношению доходности акционерного капитала к его стоимости. Если доходность акционерного капитала равна 8 % и ставка дисконтирования – 8 %, то стоимость компании всегда будет равна балансовой стоимости. Если доходность равна 10 %, а дисконт – 8 %, то при отсутствии роста коэффициент цена / балансовая стоимость будет равен 10/8 = 1,25. Теперь обратим внимание на взятую в рамку цифру стоимости в таблице при доходности собственного капитала 10 % и темпе роста 5 % – справедливая оценка коэффициента цена / балансовая стоимость равна 1,67. Это означает, что способность компании осуществлять дополнительные инвестиции, приводящие к 5 %-ному росту, создает дополнительную стоимость, этим обусловлена разница коэффициентов цена / балансовая стоимость (1,25 и 1,67).
В приводимых в этой книге примерах реальных компаний мы будем использовать обе методики расчета, но будем более тщательно разделять доходность старого и доходность нового акционерного капитала. Главное: не существует принципиального различия между оценкой компании по методу дисконтированных денежных потоков и оценкой по методу экономической прибыли.
5. Прогнозирование в реальной жизни
Разумеется, в большинстве компаний темпы роста меняются. На практике мы не способны предсказывать конкретные цифры до бесконечности, поэтому в итоге мы получаем совокупность конкретного прогноза и так называемой терминальной стоимости: будущей стоимости бизнеса на момент, когда мы прекращаем определять конкретные прогнозные значения и предполагаем, что темп роста компании становится постоянным. Общепринято, что такой момент наступает, когда компания становится зрелой и находится в середине цикла по уровню доходности и прибыльности.
Мы упомянули, но не показали, как обе методики расчета будут применяться в случаях, когда денежные потоки или доходы изменяются во времени. Дисконтированный денежный поток на собственный (акционерный) капитал компании может быть записан следующим образом:
V = Σ Dt / (1+k)t,
где Σ – сумма ряда от момента t = 0 до момента t = ∞. Альтернативный подход к оценке может быть выражен следующей формулой:
V = B0 + Σ Xt / (1+k)t,
где B0 – текущая балансовая стоимость, Xt – остаточный доход, который компания ожидает получить в году t. Xt можно записать как
Xt = Yt – Bt-1 × k,
т. е. остаточный доход – это прибыль (Y) за вычетом расходов на акционерный капитал, который использовался в бизнесе на начало года.
Мы хотели продемонстрировать, что два метода определения стоимости – дисконтированный денежный поток и балансовая стоимость на начало периода плюс дисконтированный поток остаточного дохода – всегда должны давать одинаковую оценку (доказательство дано в приложении). Объяснить это можно так: дивиденды в любой год могут быть выражены как полученные доходы минус увеличение балансовой стоимости за год. Дисконтирование дивидендов приписывает дивидендам стоимость, дисконтирование остаточного дохода приписывает стоимость доходам, но учитывает затраты на вновь привлекаемый акционерный капитал (капитализированные затраты).
Независимо от того, дисконтируем мы денежный поток на акционерный капитал в форме привычной модели дисконтирования дивидендов или поток остаточного дохода (разница между прибылью и платой за капитал) и затем прибавляем его к изначальной балансовой стоимости акционерного капитала на начало года, результаты должны совпадать.
Одно из преимуществ второго метода в том, что он не требует выбирать вид денежного потока для случая, когда вместо дивидендов используется прибыль. Начисленные доходы или выплаты в рамках концепции остаточного дохода определить несложно. Это не совсем так для моделей дисконтированных дивидендов и дисконтированного денежного потока, поскольку представляется менее логичным начинать расчет с денежного потока и затем вычитать часть его и прибавлять неполученную прибыль. Но вы должны это делать, если модель предназначена для получения обоснованной оценки. Именно поэтому многие ученые предпочитают модель, основанную на остаточном доходе.
6. Учитываем заимствования
Мы начали с рассмотрения компании с постоянным темпом роста и финансируемой только из собственных средств (акционерного капитала) и пришли к заключению, что для ее анализа достаточно данных отчета о прибыли и убытках бухгалтерского баланса. Затем мы усложнили задачу, приняв, что, какая бы модель ни использовалась, в ней должны учитываться накопленные средства. Затем мы обобщили модель, ослабив условие постоянного роста, это ничего не изменило, кроме того, что практически невозможно построить прогноз на каждый год на бесконечном горизонте. Но как бы далеко мы ни уходили в таких прогнозах, это не вызывает никаких методологических проблем, кроме применимости на практике.
Теперь снимем предположение об отсутствии задолженности (или денежных средств) на балансе компании. Понятно, что в этом случае не важно, дисконтируем мы денежные потоки, относящиеся к капиталу, по стоимости капитала, или денежные потоки, относящиеся к акционерному капиталу, по стоимости акционерного капитала. Доказательство этого факта в Приложении, а суть в следующем соотношении:
VE = VF – VD.
Эти три величины относятся, соответственно, к акционерному капиталу, к суммарному капиталу фирмы и к задолженности (заимствованному капиталу). Важно, что нет разницы, оцениваем мы акционерный капитал непосредственно как
VE = D × (1 + g) / (k – g)
или как
VE = FCF × (1 + g) / (WACC – g) – VD,
где FCF – свободный денежный поток за прошлый год, WACC – средневзвешенная стоимость капитала.
При расчете свободного денежного потока принимается, что уже вычтен налог по эффективной ставке, взимаемый с операционной прибыли (от основной производственной деятельности), и получена так называемая чистая операционная прибыль после налогообложения (NOPAT). В табл. 1.6 показан расчет NOPAT и свободного денежного потока для компании, имеющей постоянный темп роста и частично финансируемой за счет заимствований. Если расчет произведен корректно, то оценка стоимости будет такой же, независимо от того, как оценивалась компания – путем дисконтирования свободного денежного потока по средневзвешенной стоимости капитала и вычитания стоимости долга или путем дисконтирования свободного денежного потока, приходящегося на собственный (акционерный) капитал, по стоимости этого капитала (как мы поступили выше). (Взаимосвязь этих ставок дисконтирования будет проанализирована в следующей главе.)

К этому расчету необходимо сделать два важных замечания. Первое: налоговая нагрузка – эффективная, и свободные денежные потоки рассчитываются с учетом предположения, что компания полностью финансируется за счет акционерного капитала. Денежные потоки рассчитываются без учета заимствований. Второе: итог по трем статьям (амортизация, капитальные затраты и изменение оборотного капитала) в совокупности составляют чистые инвестиции компании. Эта часть NOPAT, которая реинвестируется в бизнес, а свободный денежный доход – то, что выводится из него. Для действительно не имеющей заимствований компании NOPAT равна чистому доходу, а свободный денежный поток – сумме дивидендов, что мы и предполагали в нашем упрощенном обсуждении.
Теперь оценивать компании мы можем четырьмя методами: с использованием денежного потока на акционерный капитал (дисконтирование дивидендов); денежного потока на капитал (модель дисконтированных денежных потоков DCF); экономической прибыли на акционерный капитал (остаточный доход); или экономической прибыли на капитал (модель добавленной экономической стоимости EVATM). Собственный капитал компании может быть оценен либо дисконтированием свободного денежного потока, либо поправкой балансовой стоимости с учетом экономической прибыли. Точно так же можно поступить и с капиталом компании в целом. Используя любой из этих методов, мы получим одинаковый ответ, но все варианты зависят от данных финансовой отчетности компании. Они должны корректироваться с учетом динамики накопления капитала. Абсолютно неправильно утверждать, что дисконтирование денежных потоков освобождает нас от этой обязанности.
Замечание. Подчеркнем, что из неденежных статей расходов в числитель нашей оценочной модели не включаются амортизация материальных и нематериальных активов. В модели DСF денежный поток – это NOPAT (включая изменение инвестированного капитала) минус чистые инвестиции (капитальные затраты плюс изменение оборотного капитала минус износ и амортизация). В модели экономической прибыли NOPAT также учитывается изменение инвестированного капитала. Капитал, по которому рассчитываются расходы на капитал, растет за счет капитальных затрат и оборотного капитала и уменьшается за счет амортизации. Таким образом, все неденежные элементы, кроме амортизации, должны отражаться в величине денежного потока или прибыли, которые подлежат дисконтированию, или должны быть исключены из рассмотрения. Единственное различие между двумя моделями: в модели DCF амортизация является источником денег, а в модели экономической прибыли она сокращает будущие расходы на капитал.
Глава 2
Четыре десятилетия WACC
Введение в CAРM
1. Что означают в финансовом смысле риски и доходность?
2. Как инвесторы находят оптимальную комбинацию риска и доходности?
3. Как следует оценивать вложения в различные активы – отдельно или в составе портфеля, и почему это различие важно?
4. Как определяется ставка дисконтирования денежных потоков, генерируемых тем или иным активом?
5. Источниками финансирования компаний служат заимствования и акционерный капитал; как изменение соотношения между ними влияет на ставку дисконтирования, которую эффективный рынок применит к денежным потокам этих компаний?
Последний вопрос подробно исследовали Миллер и Модильяни. Поиск ответов на первые четыре вопроса привел к появлению модели CAPM (модели оценки стоимости активов). Развитие этого направления теории инвестиций связано с именами Марковица, Шарпа и Линтнера.
1. Риск и доходность
В табл. 2.1 приведены характеристики риска и доходности трех активов: государственной облигации, акции крупной компании и купона, удостоверяющего ставку на ипподроме. Нетрудно понять, что эти активы расположены по возрастанию степени риска. Возможно, менее ясно, что доходность третьего актива не положительная, а отрицательная.
Доходностью называется средняя ожидаемая доходность (среднее арифметическое) актива, которая учитывает все возможные результаты с весами, равными степени вероятности результата. Конечно, игрок на скачках имеет шансы, поставив на аутсайдера, получить большой выигрыш, но шансы эти чрезвычайно малы. Букмекеры зарабатывают именно на том, что устанавливают ставки таким образом, чтобы с большой вероятностью выплачивать в виде призов меньше, чем собирают в виде принятых ставок. Другими словами, ожидаемая доходность купона ставки на лошадь отрицательная, что, вероятно, не новость для читателей, игравших когда-либо на скачках.

Итак, доходностью называется средняя ожидаемая доходность актива. Как можно количественно определить степень риска актива? Обычно принято определять ее как дисперсию возможных результатов. Степень риска инвестиций низкая, если результат известен или известно, что возможные результаты находятся в относительно узком диапазоне. Если множество результатов характеризуется большой неопределенностью, то степень риска инвестиций высокая. Распределение вероятностей для этих случаев показано на рис. 2.1.
Непрерывная кривая показывает все возможные результаты для инвестиций со средней ожидаемой доходностью 9 % и стандартным отклонением (мерой дисперсии исходов) 1 %. Пунктирная кривая показывает все возможные результаты для инвестиций со средней ожидаемой доходностью 11 % и стандартным отклонением 2 %.
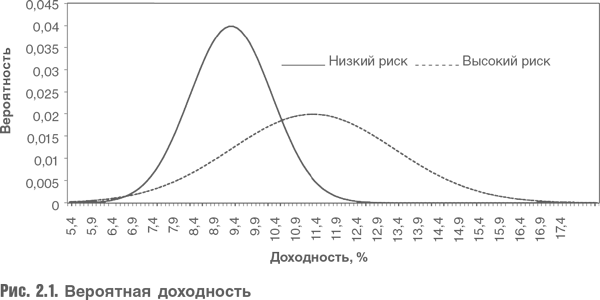
Предполагается нормальное распределение вероятностей для обоих активов (что определяет вид кривой – в форме колокола). Такое предположение не всегда верно. Безусловно, иначе обстоит дело с доходностью купонов на скачках, для которых возможны только два результата: низкая вероятность большого выигрыша, если лошадь побеждает, и высокая вероятность потерять ставку, если лошадь не выиграет.
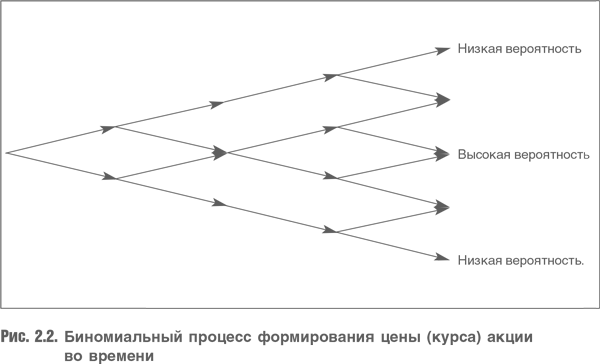
Предположение, что ожидаемая доходность имеет нормальное распределение, правомерно для активов, доходность которых складывается из малых положительных или отрицательных случайных приращений в течение продолжительной последовательности периодов, в каждом из которых вероятность выигрыша или проигрыша составляет 50 %. Такая модель достаточно хорошо описывает, что происходит с ценами акций. Обычно они периодически незначительно то растут, то снижаются согласно так называемому процессу случайного блуждания. Так постепенно складывается годовой доход. Эта особенность поведения во времени показана на рис. 2.2, где уровни подъемов и падений цен зависят от волатильности акции (измеряемой стандартным отклонением). При этом вероятность возможных результатов больше в центре распределения и ниже в его крайних точках. Когда число периодов стремится к бесконечности, результирующее распределение все больше приближается к нормальному.
2. Диверсификация и портфель инвестиций
В основе современной портфельной теории лежит предположение о том, что инвестору важны риск и доходность всего инвестиционного портфеля, а не каждого вложения в отдельности. До настоящего момента мы рассматривали каждое вложение изолированно от других. Но портфель инвестора редко состоит из единственного актива. Частные лица, например, обычно владеют домом, ценными личными вещами, денежной наличностью, являются бенефициарами активов, управляемых от их имени пенсионными фондами, имеют полисы страхования жизни, а также, возможно, владеют акциями либо напрямую, либо (чаще) через управляющие компании типа паевых или инвестиционных фондов.
Представим, что мы обладаем акциями двух компаний – British Airways (ВА) и British Petroleum (ВР). Понятно, что существует много факторов, вызывающих повышение или понижение стоимости акций этих компаний. Однако есть по крайней мере один фактор, который воздействует на цену акций обеих компаний, – цена на нефть. Повышение мировой цены на нефть будет хорошей новостью для ВР, поскольку приведет к росту ее доходов, но одновременно будет плохой новостью для ВА, поскольку увеличит ее издержки (авиационный керосин является одной из главных статей производственных расходов любой авиакомпании).
Из этого примера можно сделать два вывода. Во-первых, в случае резкого изменения цены на нефть цены акций BP и BA, скорее всего, будут меняться в противоположных направлениях. Во-вторых, инвестор, в портфель которого в определенном соотношении включены акции ВР и ВА, может не волноваться по поводу колебаний цены на нефть. В данном случае цену на нефть называют диверсифицируемым риском, поскольку владение двумя разными акциями позволяет уменьшить или полностью исключить этот фактор риска. Тот факт, что изменения цен этих акций не совпадают (или не всегда совпадают), означает, пользуясь языком статистики, что их корреляция меньше 1. Коэффициент корреляции может принимать значения от 1 для двух активов, цены которых всегда меняются в одинаковой пропорции и в одном направлении, до –1 для активов, цены которых систематически меняются в противоположных направлениях (как могли бы меняться цены акций ВР и ВА, если бы цена на нефть была единственным фактором, влияющим на их стоимость).
На рис. 2.3 показаны портфели, которые можно сформировать путем инвестирования в два актива со следующими характеристиками: А – ожидаемая доходность 15 %, стандартное отклонение 4 %, Б – ожидаемая доходность 9 %, стандартное отклонение 3,5 %. Если бы корреляция между ожидаемыми доходностями А и Б была абсолютной, то область доступных портфелей описывалась бы прямой линией, соединяющей точки А и Б.
Однако последнее предположение вряд ли правомерно, поскольку корреляция доходностей любых двух акций не может равняться 1, как мы видели при обсуждении примеров с акциями BP и BА. Нередко их цены изменяются независимо друг от друга или даже систематически меняются в противоположных направлениях. Кривая, представляющая на рис. 2.3 возможный инвестиционный портфель из акций А и Б, была построена исходя из предположения о довольно низкой корреляции 0,3 между ожидаемыми доходностями этих акций. Комбинация акций А и Б с наименьшей степенью риска (стандартное отклонение примерно 3 %) менее рискованная, нежели любая из отдельно взятых акций, и предлагает доходность примерно 11,5 %, что примерно на 2,5 % выше доходности менее рискованной акции Б, если рассматривать ее изолированно (однако меньше доходности более рискованной акции А, также взятой в отдельности). Формула стандартного отклонения для портфеля из двух акций записывается так:
SDAB = (WA² × SDA² + WB² × SDB² + 2 × WA × WB × SDA × SDB × RAB)0,5.
Вывод данной формулы приводится в любом стандартном учебнике по статистике. Безусловно, в реальности возможности выбора активов для включения в портфель гораздо шире, даже если выбор осуществляется только среди акций. Для любой группы ценных бумаг можно построить огибающую линию, получаемую путем изменения их относительных весов в портфеле. Такая огибающая задает границу области достижимых комбинаций риска и доходности. Очевидно, что эффективным будет портфель, который располагается левее и выше всех других достижимых портфелей на графике (высокая доходность и низкий риск).
Именно к этому выводу пришел Марковиц в своем анализе. Полноценная модель САРМ была создана позднее, в частности, в трудах Шарпа и Линтнера.
Отправная точка модели САРМ: при увеличении количества разных акций в портфеле его волатильность уменьшается, пока не достигает неснижаемого минимума – волатильности портфеля акций фондового рынка в целом. На рис. 2.4 показано, как изменяется волатильность портфеля акций при увеличении количества разных акций в нем. По мере того, как специфические для каждой отдельной акции риски диверсифицируются, единственным недиверсифицируемым риском портфеля остается так называемый рыночный или систематический риск.




