
Яков Перельман
Занимательная физика. Книга 2
Безостановочная железная дорога
Когда вы стои́те на неподвижной платформе и мимо нее проносится курьерский поезд, то вскочить в вагон на ходу, конечно, мудрено. Но представьте, что платформа под вами также движется, при том с такою же скоростью и в ту же сторону, как и поезд. Трудно ли вам будет тогда войти в вагон?
Нисколько: вы войдете так же спокойно, как если бы вагон стоял неподвижно. В самом деле: раз и вы и поезд движетесь в одну сторону с одинаковой скоростью, то по отношению к вам поезд находится в полном покое.
Правда, колеса его вращаются, но вам будет казаться, что они вертятся на одном месте.
Следовательно, вполне мыслимо устроить так, чтобы поезд, проходя мимо станций, принимал и высаживал пассажиров на полном ходу, не останавливаясь.
Приспособления такого рода нередко устраиваются на выставках, чтобы дать публике возможность быстро и удобно осматривать их достопримечательности, раскинутые на обширном пространстве. Так, на международной архитектурной выставке в Лейпциге осенью 1913 года крайние пункты выставочной площади были, словно бесконечной лентой, соединены железной дорогой; при этом пассажиры могли в любой момент и в любом месте входить в вагоны и выходить из них на полном ходу поезда.
Схема этого любопытного устройства видна на прилагаемых рисунках. На рис. 4 буквами А и В отмечены крайние станции. На каждой станции помещается круглая неподвижная платформа, окруженная большим вращающимся кольцеобразным диском. Вокруг вращающихся дисков обеих станций проходит канат, к которому прицеплены вагоны. Теперь проследите, что происходит при вращении платформы. Вагоны обегают вокруг платформ с такою же скоростью, с какою вращаются внешние края платформ; следовательно, пассажиры без малейшего опасения могут переходить с платформ в вагоны или, наоборот, покидать поезд. Выйдя из вагона, пассажир идет к центру круга, пока не дойдет до неподвижной платформы; а здесь перейти с внутреннего края подвижного диска на неподвижный уже нетрудно, так как при малом радиусе круга весьма мала и скорость вращения[6]. Достигнув внутренней, неподвижной платформы, пассажиру остается лишь перебраться по мостику на землю вне железной дороги (рис. 5).
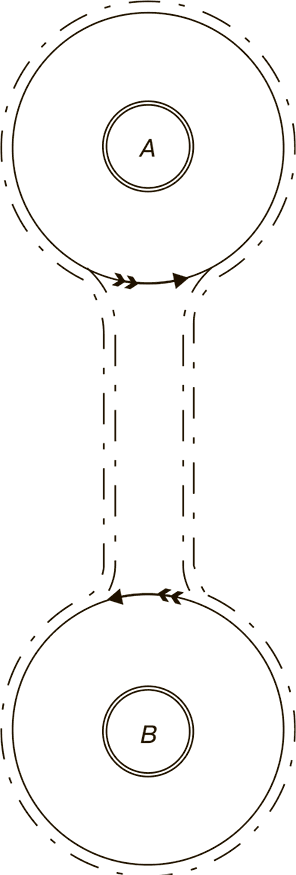
Рис. 4. Как была устроена «безостановочная» железная дорога на Лейпцигской выставке. Дорога обозначена пунктиром. А и В – вокзалы.
Рис. 4 и 5 поясняют сказанное. Размеры кругов и скорость их вращения выбраны были так, что внешние края их пробегали две сажени[7] в секунду (около 16 верст в час), внутренний же край двигался со скоростью всего полусажени в секунду; при такой скорости – вернее сказать, при такой медленности – можно было, разумеется, вполне безопасно переходить на платформу.
Отсутствие частых остановок дает огромный выигрыш во времени и затратах силы. Во всяком трамвае большая часть времени и чуть не ⅔ всей энергии тратится на постепенное ускорение движения при отходе со станции, а также на замедление и торможение при остановках.
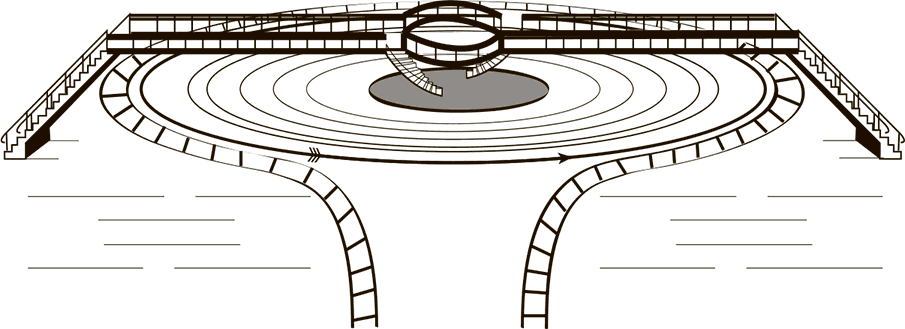
Рис. 5. Вокзал безостановочной железной дороги.
Через круглую, вечно вращающуюся платформу перекинута галерея, по которой пассажиры спокойно переходят из внутреннего, неподвижного круга на землю вне дороги.
На станциях железных дорог можно было бы обойтись даже без специальных подвижных платформ, чтобы принимать и высаживать пассажиров на полном ходу поезда. Вообразите, что мимо обыкновенной неподвижной станции проносится курьерский поезд; мы хотим, чтобы он, не останавливаясь, принял здесь новых пассажиров. Пусть же эти пассажиры займут пока места в другом поезде, стоящем на запасном параллельном пути, и пусть этот поезд начнет двигаться вперед, стремясь развить ту же скорость, что и курьерский. Необходимо устроить так, чтобы, когда оба поезда будут идти рядом, скорости их сравнялись. В этот момент оба поезда будут словно неподвижны один относительно другого: достаточно перекинуть мостки, которые соединяли бы вагоны соседних поездов, – и пассажиры «временного» поезда могут спокойно перейти в курьерский. Остановки на станциях сделаются, как видите, излишними.
Такова теория. Осуществление этого проекта на практике, вероятно, очень хлопотливо; потому-то ничего подобного нигде пока не устраивалось.
Улицы будущего
Не осуществлено на практике еще и другое приспособление, основанное на том же законе относительного движения: так называемые «движущиеся тротуары».
Вот чертеж такого устройства (рис. 6). Вы видите пять замкнутых полос-тротуаров, движущихся посредством особого механизма, одна внутри другой, с различной скоростью. Самая крайняя полоса ползет довольно медленно – со скоростью всего 5 верст в час; это скорость обыкновенного пешехода, и, понятно, вступить на такую медленно ползущую полосу не трудно даже ребенку или старику. Рядом с ней, внутри, бежит вторая полоса, со скоростью 10 верст в час. Вскочить на нее прямо с неподвижной улицы было бы очень опасно, но зато перейти на нее с первой полосы – ничего не стоит. В самом деле, по отношению к этой первой полосе, ползущей со скоростью 5 верст, вторая, бегущая с 10-верстной быстротой, делает ведь только 5 верст; значит, перейти с первой на вторую столь же легко, как перейти с земли на первую. Далее, третья полоса движется уже с 15-верстной скоростью, – но перейти на нее со второй полосы, конечно, нетрудно. Так же легко перейти с третьей полосы на следующую, четвертую, бегущую с 20-верстной скоростью, и, наконец, с нее на пятую, мчащуюся со скоростью 25 верст в час. Эта пятая полоса доставляет пассажира до того пункта, который ему нужен; здесь, спокойно переходя обратно с полосы на полосу, он высаживается на неподвижную землю.

Рис. 6. Движущиеся тротуары.
Такую непрерывно движущуюся улицу-поезд предполагалось устроить в Нью-Йорке, в подземном туннеле. Эта железная дорога представляла бы собой непрерывную круговую ленту с устроенными на ней сиденьями для пассажиров; лента движется, согласно проекту, со скоростью 21 версты в час. К ней примыкают еще три вспомогательные ленты, облегчающие переход с неподвижной почвы на ленту-поезд. Скорости их – 16, 10½ и 5 верст в час. Пассажиру, желающему сесть в поезд, нетрудно вступить с неподвижного пола на первую ленту (держась за один из ее вертикальных стержней); так же легко перейти с нее на вторую ленту, затем на третью, и, наконец, сесть в поезд.

Рис. 7. Движущаяся улица-поезд под землей. Перед тем как попасть с неподвижной платформы в поезд, пассажиры проходят через три полосы, движущиеся вперед, каждая немного быстрее предыдущей.
Непостижимый закон
Ни один из законов механики не вызывает, вероятно, столько недоумений, как знаменитый «третий закон Ньютона» – закон равенства действия и противодействия. Все его знают, умеют даже, когда нужно, правильно применять его – и все-таки мало кто верит в его истинность. Может быть, вы имели счастье, читатель, сразу понять его, – но что касается меня, то, должен сознаться, я постиг его много лет спустя после моего первого с ним знакомства. Я расспрашивал разных лиц, имеющих более или менее близкое отношение к механике, и убедился, что большинство из них готовы признать правильность этого закона лишь с довольно существенными оговорками. Охотно допускают, что он верен для тел неподвижных, но не понимают, как можно применять его к взаимодействию движущихся тел…
«Действие, – гласит этот закон, – всегда равно и противоположно противодействию». Это значит, что когда, например, лошадь тянет телегу, то телега тянет лошадь назад с точно такою же силою, с какою лошадь тянет телегу вперед. Но если так, то выходит, что телега должна оставаться на месте; почему же она все-таки движется? Почему лошадь увлекает телегу, а не телега увлекает лошадь назад? Ведь они тянут друг друга с одинаковой силой… И почему эти силы не уничтожаются взаимно, если они равны?
Эти недоумения разрешаются довольно просто. Силы не уничтожают друг друга потому, что приложены к разным телам: одна – к телеге, другая – к лошади. Силы эти равны, да, – но разве одинаковые силы всегда производят одинаковые действия? Разве равные силы сообщают всем телам равные скорости? Разве действие силы на тело не зависит также и от самого тела, – от величины того сопротивления, которое тело оказывает силе?
Если подумаете об этом, вам сразу станет понятно, почему лошадь все же увлекает телегу, хотя телега тянет ее обратно с такою же силою. Сила, действующая на телегу, и сила, действующая на лошадь, равны; но так как телегу гораздо легче заставить катиться, чем волочить назад идущую лошадь, то вполне понятно, что телега катится в сторону лошади, а не лошадь притягивается к телеге. Поясним на числовом примере. Пусть лошадь тянет телегу с силою 20 пудов[8]; следовательно, и телега тянет к себе лошадь с силою 20 пудов. Для того, чтобы сообщить телеге некоторую скорость, сила в 20 пудов достаточна; но она далеко не достаточна, чтобы сообщить обратную скорость лошади, которая уже привела себя в движение по направлению вперед. Натягивая постромки и отталкиваясь ногами от земли, лошадь, в общем, развивает силу не в 20 пудов, а бóльшую – пудов в 30, скажем. Часть этой силы – 10 пудов – сообщает самой лошади движение вперед, а остальная часть, 20 пудов, преодолевает сопротивление телеги и приводит ее в движение. Закон равенства действия и противодействия здесь не нарушается: сила в 20 пудов, приложенная к телеге, вызывает равную противодействующую силу со стороны телеги, а сила в 10 пудов, с которой лошадь отталкивается от земли, вызывает равное противодействие со стороны земли.
Даже падение тел строго подчиняется закону равенства действия и противодействия. Яблоко падает на землю оттого, что его притягивает земной шар. Но с точно такою же силою и яблоко притягивает к себе нашу планету. Строго говоря, яблоко и Земля падают друг на друга, но скорость этого падения различна для яблока и для Земли. Одна и та же сила взаимного притяжения сообщает яблоку ускорение в 5 сажень, а земному шару – во столько раз меньше, во сколько раз масса Земли превышает массу яблока. Конечно, масса земного шара в неимоверное число раз больше массы яблока, и потому Земля получает перемещение настолько ничтожное, что практически его можно считать равным нулю. Оттого-то мы и утверждаем, что яблоко падает на землю, вместо того, чтобы говорить: «яблоко и Земля падают друг на друга».
Отчего погиб Святогор-богатырь?
Вы помните былину о Святогоре-богатыре, который вздумал поднять Землю? Архимед, если верить преданию, тоже намеревался, не будучи богатырем, совершить такой подвиг и искал лишь точки опоры для своего рычага. Позднее мы побеседуем о том, какой непредвиденный сюрприз ожидал бы гениального математика, если бы ему была дана эта желанная точка опоры. Но Святогор был силен и без рычага. Он мечтал лишь о том, чтобы было за что ухватиться, к чему приложить свои богатырские руки. Случай представился: богатырь нашел на земле «сумочку переметную», в которой сосредоточена была «вся тяга земная». Ухватившись за нее, Святогор стал тянуть вверх изо всей силы. Но сумочка не поддалась – зато сам Святогор по колено в землю увяз. «Тут ему было и кончание».
Если бы Святогору был известен закон равенства действия и противодействия, он сообразил бы, что его богатырская сила, приложенная к Земле, вызовет равную, а, следовательно, столь же колоссальную противодействующую силу, которая может втянуть его самого в землю.
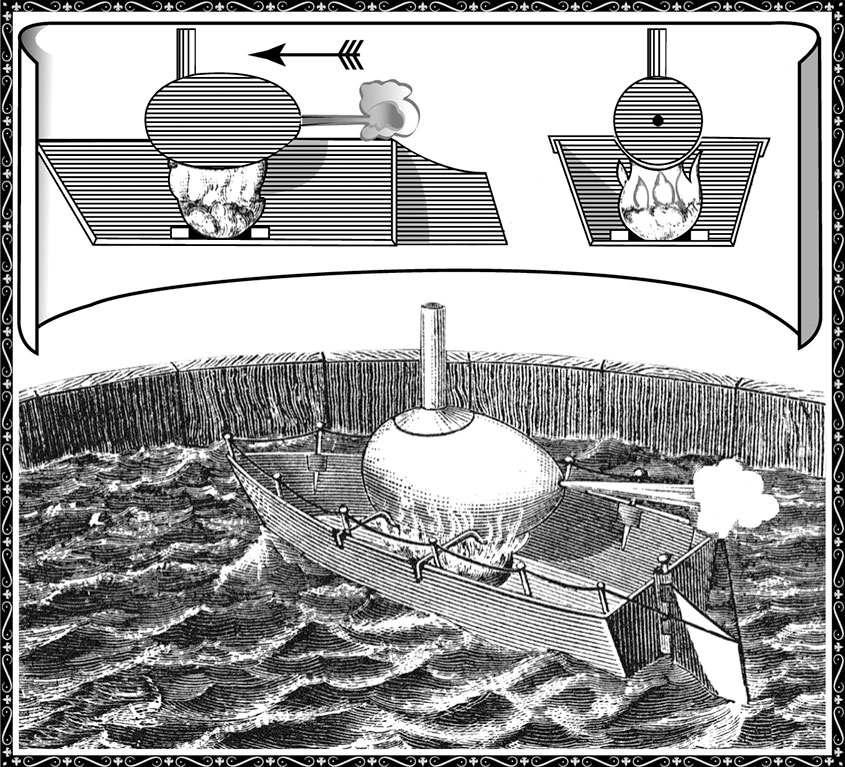
Рис. 8. Игрушечный пароходик из пустого яйца и бумаги, наглядно доказывающий, что «действие равно противодействию». В яйцо наливают воды, и этот миниатюрный паровой котел подогревается горением намоченной в спирте ваты.
Когда из отверстия в яйце начинает бить струя пара, весь пароходик, силою возвратного толчка, движется в противоположном направлении.
Во всяком случае, из былины видно, что народная наблюдательность давно подметила противодействие, оказываемое Землей, когда на нее опираются. Народ бессознательно применял закон равенства действия и противодействия за тысячелетия до того, как Ньютон впервые сформулировал его в своей бессмертной книге «Математические основы натуральной философии» (т. е. физики).
Можно ли двигаться, ни на что не опираясь?
Когда человек ходит, он отталкивается ногами от земли или от пола; все знают, что по очень гладкому полу, от которого нога не может оттолкнуться, ходить нельзя. Паровоз при движении отталкивается колесами от рельсов: если рельсы смазать маслом, паровоз останется на месте. Пароход лопастями своего винта отталкивается от воды. Аэроплан отталкивается от воздуха также при помощи винта – пропеллера. Словом, в какой бы стихии ни двигался предмет, он опирается на нее при своем перемещении. Но может ли тело двигаться, не имея никакой опоры вне себя?
Казалось бы, такое движение невозможно, и стремиться к нему все равно, что желать поднять самого себя за волосы. Но это только кажется: именно такое будто бы невозможное движение часто происходит на наших глазах. Правда, тело не может привести себя целиком в движение одними лишь внутренними силами, но оно может заставить некоторую часть своей массы двигаться в одну сторону, остальную же – в другую, противоположную. Сколько раз видели вы летящую ракету, – а задумывались ли над вопросом: почему она летит? Между тем, в ракете мы имеем прекрасный пример того рода движения, которое сейчас нас интересует.
Почему взлетает ракета?
Даже среди людей науки приходится нередко слышать превратное объяснение полета ракеты: она летит, мол, потому, что своими газами (которые образуются при горении пороха внутри нее) она отталкивается от воздуха. Однако, если пустить ракету в безвоздушном пространстве, она полетит нисколько не хуже, пожалуй, даже лучше, чем в воздухе. Истинная причина движения ракеты состоит в том, что, когда пороховые газы стремительно вытекают из нее вниз, сама трубка ракеты, по закону равенства действия и противодействия, отталкивается вверх. Здесь, в сущности, происходит то же, что и при выстреле из пушки: ядро летит вперед, а сама пушка отталкивается назад. Вспомните «отдачу» ружья и всякого вообще огнестрельного оружия! Если бы пушка висела в воздухе, ни на что не опираясь, она после выстрела двигалась бы назад с некоторой скоростью, которая во столько же раз меньше скорости ядра, во сколько раз ядро легче самой пушки. Когда 12-дюймовая[9] пушка, установленная в башне современного дредноута[10], извергает из своего жерла 30-пудовое ядро со скоростью 400 саженей в секунду, – все огромное судно, весящее более миллиона пудов, отталкивается назад со скоростью одного дюйма в секунду. Основываясь на том же правиле механики, герои романа Жюля Верна «Вверх дном» задумали «выпрямить» земную ось выстрелом из колоссальной пушки. Ракета – та же пушка, только извергает она не ядра, а пороховые газы.
По той же причине вертится и так называемое «китайское колесо»: при горении пороха в трубках, прикрепленных к колесу, газы вытекают в одну сторону, сами же трубки (а с ними и колесо) получают обратное движение.

Рис. 9. Плавающая рыбка, вырезанная из визитной карточки. Это маленькое изобретение Тома Тита основано на законе противодействия: если в вырезанный кружок а капнуть масла, то, свободно растекаясь по воде вдоль канала от а к b, масляная пленка будет оказывать давление в обратную сторону и заставит рыбку двигаться в направлении ее головы.
Есть множество игрушек, основанных на этом начале. Игрушечный пароход (Рис. 8.), изобретенный остроумным Томом Титом, движется потому, что пар, вытекая в одну сторону, толкает весь пароход в обратную. Если в прорезь картонной рыбки, положенной на воду (см. рис. 9), капнуть масла, она поплывет в направлении, обратном тому, по которому растекается масляная пленка. Наконец, мы знаем, что самая древняя в мире паровая машина, изобретенная Героном Александрийским еще в III век до Р. X., была устроена по тому же принципу: пар из котла αβ (рис. 10) поступал по трубке εζη в шар, вращающийся на горизонтальной оси; вытекая затем из коленчато-изогнутых трубок, пар толкал эти трубки в обратном направлении, – и шар начинал вращаться. К сожалению, Геронова паровая турбина в древности оставалась только любопытной игрушкой, не более, так как дешевизна труда живых двигателей – рабов – никого не понуждала к практическому использованию мертвых машин.

Рис. 10. Самая древняя в мире паровая машина (турбина), изобретенная Героном Александрийским в III веке до Р. X.
Как движется каракатица?
Вероятно, вам странно будет слышать, что существует множество живых существ, для которых мнимое «вытаскивание самого себя за волосы» является весьма обычным способом перемещения.
Каракатица и вообще большинство головоногих моллюсков движутся в воде таким образом: они набирают воду в жаберную полость через боковую щель и особую воронку впереди тела и затем энергично выбрасывают струю воды через упомянутую воронку; при этом они получают обратный толчок, достаточный для того, чтобы довольно быстро плавать задней стороной тела вперед. Каракатица может, впрочем, направить трубку воронки вбок или назад и, энергично выдавливая из нее воду, двигаться в любом направлении.
На том же основано и движение медузы: сокращением мускулов она выталкивает из-под своего колоколообразного тела воду, получая толчок в обратном направлении. Сходным приемом пользуются при движении сальпы, личинки стрекоз и многие другие водные животные. А мы еще сомневались, можно ли так двигаться!

Рис. 11. Как передвигается в воде каракатица. С силою выбрасывая из своего тела набранную воду, животное получает толчок, который и относит его назад.
К звездам на ракете
Что может быть заманчивее, чем покинуть наш земной шар и путешествовать по необъятной вселенной, перелетать с планеты на планету, со звезды на звезду? Сколько фантастических романов написано на эту тему! Кто только не увлекал нас в воображаемое путешествие по небесным светилам! Вольтер в «Микромегасе», Жюль Верн в «Путешествии на Луну» и «Гектор Сервадак», Уэллс в «Первых людях на Луне» и множество их подражателей совершали воображаемые путешествия на небесные светила, – конечно, в мечтах. В действительности же мы – увы! – остаемся пленниками земного шара[11].
Неужели же нет возможности осуществить эту давнишнюю мечту человечества? Неужели все остроумные проекты, с такой заманчивой правдоподобностью изображенные в романах, на самом деле неисполнимы? В дальнейшем мы еще будем беседовать о фантастических проектах межпланетных путешествий; теперь же познакомимся с единственным серьезным проектом подобных путешествий, предложенным русским ученым К. Э. Циолковским.
Можно ли долететь до Луны на аэроплане? Конечно, нет: аэропланы и дирижабли движутся только потому, что опираются о воздух, отталкиваются от него, – а между Землей и Луной воздуха нет. В межпланетном пространстве вообще нет никакой материальной среды, на которую мог бы опереться «межпланетный дирижабль». Значит, надо придумать такой снаряд, который мог бы двигаться, ни на что не опираясь.

Мы уже знакомы с подобным снарядом в виде игрушки – это ракета. Так отчего бы не устроить огромную ракету, с особым помещением для людей, съестных продуктов, запасов воздуха и всем прочим? Вообразите, что люди в этой ракете везут с собой большой запас взрывчатых веществ и, подобно каракатице, могут направлять истечение газов в любою сторону. Вы получите настоящий управляемый небесный корабль, на котором можно плыть в беспредельном океане мирового пространства, полететь на Луну, на планеты, к звездам… Пассажиры могут посредством ряда отдельных мелких взрывов увеличивать скорость этого межпланетного дирижабля с необходимой постепенностью, чтобы возрастание скорости было безвредно для них. При желании спуститься на какую-нибудь планету они могут постепенно уменьшить скорость снаряда и тем ослабить силу падения. Наконец, пассажиры могут таким же путем возвратиться и обратно на Землю. Для всего этого надо только захватить с собой достаточный запас взрывчатых веществ.
«Зачем же дело стало? – спросите вы. – Почему же никто не сооружает такой гигантской ракеты и не отправляется исследовать глубины межзвездных пространств?»
Остановка в том, что мы пока не имеем достаточно сильного взрывчатого вещества. Чтобы сообщить исполинской ракете скорость, потребную для преодоления силы тяжести, нужно взрывчатое вещество силою в 10–15 раз больше, чем у пироксилина[12]. Такого вещества мы еще не знаем; не имеем мы и достаточно крепких материалов для «небесной ракеты».
Но то, что невозможно сегодня, может осуществиться завтра. Человечество уже было однажды в подобном положении: когда найден был принцип летания по способу парения, для сооружения аэроплана не хватало лишь достаточно сильного двигателя и достаточно прочных материалов. Прошло 15 лет, – и что же? Аэропланы высоко реют в воздухе, перелетая через горы и моря; мы присутствовали уже и при воздушной войне… Так отчего не допустить, что когда-нибудь люди полетят к звездам в огромном ракетообразном снаряде?






