
Полина Лосева
Против часовой стрелки. Что такое старение и как с ним бороться
Считаем мутации
Когда на лекциях я спрашиваю у слушателей, что такое старость, мне часто отвечают: это поломки и нарушения в организме. В это определение вписывается и репродуктивный критерий: неспособность размножаться – одна из таких поломок. Но, поскольку она может возникнуть у каждого конкретного человека раньше или позже, вне связи с другими признаками старения, делать ее мерилом старости неразумно, если мы хотим найти единую для всех точку отсчета.
Можно составить список неполадок, характерных для старого организма. По такому принципу работают "индексы хрупкости"[3] (мы вернемся к ним в главе, посвященной биологическому возрасту), которые часто используют медики, изучающие старение. Индекс хрупкости – это набор симптомов и возрастных заболеваний, которые накопил в себе тот или иной пациент. Чем выше значение индекса, тем ближе к старости.
С индексом может произойти та же неприятность, что и с внешними признаками старости: когда мы ориентируемся на следствия, а не причину, богатые люди оказываются в среднем моложе своих бедных сверстников. Это, впрочем, не значит, что проблему старения можно просто "залить деньгами": в конечном счете богачи умирают так же, как и бедняки, и не меньше заинтересованы в продлении жизни. Поэтому нам придется смотреть глубже – в отдельные клетки и молекулы, и искать признаки старения уже на микроскопическом уровне.
Образцом молекулярной приметы старости можно считать точечную мутацию в ДНК, то есть замену одной "буквы" (нуклеотида) в ее "тексте" (последовательности) на другую. В большинстве случаев такие единичные замены не влияют на жизнь клетки, поскольку генетический код избыточен и застрахован от случайных ошибок. Однако поломка может возникнуть и в значимом месте гена – тогда он либо прекратит работать совсем, либо белок, который он кодирует, получится деформированным. Мутантный белок иногда выполняет свои функции лучше или хуже обыкновенного, и в обоих случаях это может привести к неприятным последствиям для организма, вроде развития опухоли.
Не все точечные мутации сказываются на жизни организма, но определить эффект, который производит каждая из них в отдельности, довольно сложно. Поэтому для простоты можно любую точечную мутацию рассматривать как поломку. В конце концов, любая из них делает ДНК в клетке отличной от "оригинала", исходного носителя генетической информации.
В 2018 году вышли статьи сразу у двух[4] групп[5] ученых, которые считали точечные мутации в нервных клетках людей. Исследователей интересовало, в какой момент эти мутации возникают и сколько их накапливается за время жизни. Для этого они брали несколько соседних нервных клеток из головного мозга взрослых людей – и зачатка мозга у зародышей (ученые работали с материалом, полученным в результате абортов) и прочитывали их ДНК. В идеале во всех клетках нашего организма последовательность нуклеотидов в ДНК должна быть одинакова. Но в течение жизни каждая клетка независимо от других накапливает "однобуквенные" замены. Поэтому, если сравнить две клетки между собой, количество точечных отличий в тексте ДНК и будет равно количеству мутаций в каждой клетке.
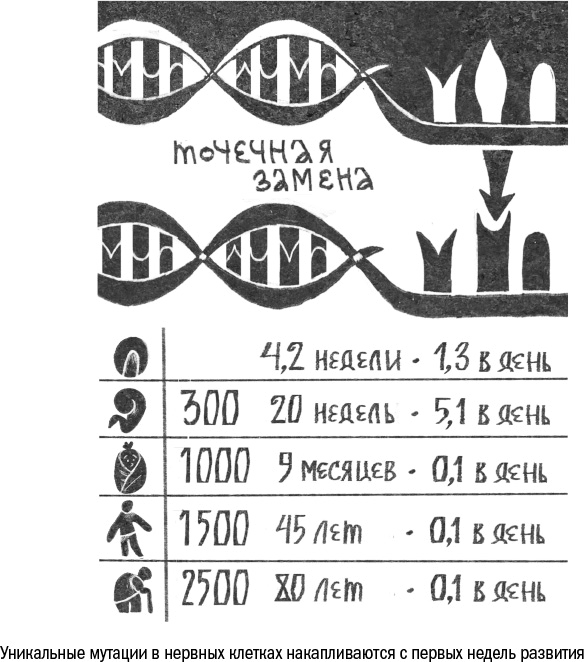
Результаты подсчетов получились устрашающими. В самом начале развития эмбриона, когда оплодотворенная яйцеклетка дробится на первые клетки, она делится примерно раз в сутки. Каждое такое деление, как оказалось, уже приносит с собой в среднем 1,3 новых мутаций. Позже, когда начинает формироваться нервная система – к 15 неделе развития, – каждый день добавляет клеткам еще около пяти мутаций. И к окончанию нейрогенеза, то есть деления клеток в большинстве областей развивающегося мозга – это примерно 21 неделя, – каждая клетка несет в себе уже 300 уникальных точечных мутаций. К рождению человека в тех клетках, которые продолжают делиться, накапливается до 1000 мутаций. А дальше, в течение жизни, ДНК мутирует медленнее, со скоростью около 0,1 ошибки в день, и к 45 годам клетки содержат примерно по 1500 мутаций, а к 80 годам – по 2500.
Если мы, как и условились, считаем каждую мутацию поломкой, то есть признаком старости, то получается, что человек начинает стареть сразу после зачатия, с момента первого деления оплодотворенной яйцеклетки. Но как может дряхлеть структура, которая еще не сформировалась?
На молекулярном уровне наши интуитивные представления о старении подтверждаются: это не событие, а непрерывный процесс. Мутации не возникают вдруг, а копятся с первого дня развития и до конца жизни. И где провести границу "молодости ДНК", совершенно непонятно. Если отсчитывать старость от появления самой первой мутации, то придется признать состарившейся кучку из нескольких клеток. А если попробовать установить пороговое значение для числа мутаций, то мы столкнемся с той же проблемой, что и в случае с пенсионным возрастом: чтобы граница не вызывала у нас удивления, придется опереться на другие признаки старости – внешность, способность размножаться или что-то еще, – которые, как мы уже знаем, недостоверны.
Можно было бы ориентироваться не на момент появления ошибок, а на скорость мутирования – например, назвать старым того, у кого мутации начинают появляться быстрее. Но и здесь нас ждет подвох: нервные клетки до рождения копят ошибки быстрее, чем после. К моменту появления на свет они содержат уже больше трети всех мутаций, которые успеют получить за всю жизнь. Можно было бы решить, что это особенность клеток нервной ткани, которые почти полностью формируются в зародышевом периоде, а потом, после появления ребенка на свет, почти не размножаются. Но нет, делящиеся клетки кишечника или печени у взрослого человека мутируют примерно с такой же[6] скоростью, как и нервные, – около 0,1 ошибки в день. И значит, подсчет ошибок не приближает нас к определению старости.
Ставим диагноз
Кажется, однозначно определить старость и старого человека у нас не получится: старение – процесс постепенный, с концом, но без начала. Тем не менее есть люди, которые продолжают бороться со старением, несмотря на отсутствие определений, – это врачи. Они распознают старость по конкретным проявлениям: возрастным заболеваниям, и борются – когда это возможно – непосредственно с ними. Все, что сегодня врач может сделать для пожилого пациента: заменить зубы, вставить слуховой аппарат, подлечить сердце или пересадить роговицу – мелкий ремонт тела, замена отдельных деталей. Поэтому старость с точки зрения врача – это совокупность наиболее часто встречающихся дефектов, которые можно исправить.
Стоит отдать медицинскому подходу должное: пока что это самый эффективный способ продления жизни, которым мы располагаем. Какими бы ни были глубинные механизмы старения, с ними бороться мы еще не умеем, зато многие непосредственные причины смерти побеждаем легко: жители развитых стран больше не гибнут массово от инфекций, паралич давно перестал быть приговором, а справиться с повышенным давлением или уровнем сахара в крови теперь можно с помощью таблетки. Средняя продолжительность жизни за последний век выросла[7] почти в два раза. В этом смысле битва со старостью, невзирая на отсутствие четкого определения врага, уже идет полным ходом.
Но когда мы говорим об отмене старения, мы едва ли представляем себе вечную борьбу с возрастными заболеваниями. Нам, скорее всего, хотелось бы, чтобы они даже не возникали. Поэтому таблетку от старости, если мы ее придумаем, нужно будет, видимо, принимать еще до появления тревожных симптомов. А это значит, что таблетка должна будет бороться с заболеванием, которого еще нет. То, что сейчас называется "старостью" в Международной классификации болезней[8] (документе, который раз в 10 лет публикует Всемирная организация здравоохранения для унификации медицинских диагнозов в разных странах), описывает стандартный набор возрастных симптомов: "старческий возраст, старческая слабость, старческая астения". Но само по себе старение современная медицина болезнью не считает.
Хорошо это или плохо – вопрос спорный. С одной стороны, такое положение дел всерьез тормозит развитие науки. Даже если геронтологи договорятся о том, кого считать старым, а кого молодым, сейчас они не могут провести клинические испытания ни одной таблетки от старости и проверить, работает она или нет. На такое испытание они не получат ни денег, ни разрешения этических комитетов. Чтобы обойти эту проблему, они испытывают препараты против какого-нибудь возрастного заболевания – например, воспаления суставов. Если у пациентов перестанут болеть суставы, это в любом случае будет хорошо. А если они вместе с этим проживут дольше среднего – будет еще лучше.
С другой стороны, давайте представим себе, что старость все-таки официально причислят к болезням. Тогда сразу выяснится, что существенная часть населения земного шара больна, причем неизлечимо. А если измерять старение количеством мутаций, то больны окажутся поголовно все. С точки зрения медика это абсурд: болезнь есть отклонение от нормы, а где искать норму, когда здоровых людей не существует?
Пока геронтологам и врачам договориться не удалось: первые публикуют[9] призывы признать старение болезнью, вторые упорно сопротивляются. Впрочем, подозреваю, медикам рано или поздно придется сдаться: то здесь, то там отдельные биохакеры начинают экспериментировать на себе сами, а отважные исследователи запускают частные клинические испытания таблеток от старости на деньги самих испытуемых. Бороться с этим хаосом бесполезно, поэтому однажды медицинскому сообществу придется его возглавить и признать старость одной из множества болезней человечества, а заодно и договориться о едином определении.

2. Старение в числах: О чем говорят графики
Многие биологи (кроме разве что биоинформатиков) часто не любят математику. Еще школьниками они с трудом сдают вступительный экзамен в университет, а потом их отчисляют из-за нее в первую же сессию. У меня с математикой сложились на удивление неплохие отношения, но время от времени я все же обнаруживаю в себе какое-то недоверие к числам и графикам. Особенно остро оно проявляется, когда кто-нибудь пытается просчитать, как работает живой организм. Есть даже такая шутка среди биологов: "Возьмем идеальную крысу массой один килограмм…" – пародия на тех, кто пытается уместить сложные живые системы в красивые круглые цифры.
Математики, впрочем, не остаются в долгу и упрекают биологов в расплывчатых высказываниях и неконкретных суждениях. Главный проповедник скорой победы над старением и разработчик проектов косметического ремонта человеческого тела Обри ди Грей тоже математик по образованию. Оттуда, вероятно, родом и его "инженерный" подход к человеческому телу: зачем рассуждать об абстрактных причинах и закономерностях, если есть конкретные поломки, которые нуждаются в ремонте?
Если все аккуратно посчитать, говорят математики, сталкиваясь с биологической проблемой, то решение окажется простым, а долгие рассуждения – излишними. Иногда они оказываются правы. Например, когда речь заходит об определении старости, их подход действительно выглядит более эффективным. По крайней мере, именно его можно встретить в большинстве современных работ по геронтологии. В этой главе мы посмотрим, как можно описать старение в числах и какие выводы из этих чисел делают для себя биологи.
Роковая кривая
Мы воспринимаем старость как дорогу к смерти: чем старше человек, тем меньше ему осталось жить. Или, переводя на язык математики: пожилой человек с большей вероятностью умрет в ближайшее время от естественных причин (то есть от любой болезни), чем молодой.
Официальное подтверждение эта зависимость впервые получила[10] в 1825 году благодаря английскому математику Бенджамину Гомперцу. В середине жизни Гомперц начал работать на страховую компанию и заинтересовался тем, как предсказать для каждого конкретного человека риск внезапной смерти. Для этого он собрал статистические данные по смертности в нескольких городах Англии и подсчитал вероятность смерти от естественных причин для каждого возраста.
Делал он это так: допустим, в городе живут х человек 75 лет и y человек 76 лет. Тогда риск смерти (Гомперц называл его mortality intensity, то есть силой смертности) для среднестатистического человека 75 лет будет равен (x – y): x, то есть доле людей, которые умирают в 75 лет, не дожив до 76. Собрав данные и подсчитав величину риска для каждого возраста, Гомперц пытался найти закономерность, которая могла бы предсказать, как число жителей определенного возраста сокращается со временем.
Он обнаружил, что риск смерти хорошо описывается формулой: F (x) = Bqx, где х – это возраст человека, а B и q – коэффициенты (то есть постоянные числа, которые сами по себе не имеют биологического смысла; Гомперц их подобрал опытным путем, чтобы уравнять правую и левую части формулы). Таким образом Гомперц выяснил, что риск умереть растет с возрастом, причем не равномерно, а по экспоненте – то есть чем дальше, тем быстрее.
Чуть позже к разработке формулы смертности присоединился другой английский математик – Уильям Мейкхем. В 1867 году он добавил[11] к формуле Гомперца независимую от возраста компоненту С: F (x) = Bqx + С. Она отражает некоторый фоновый уровень смертности, который есть даже у новорожденного: когда возраст равен нулю, вероятность умереть нулю не равна, F (x) = C. Поэтому теперь эту формулу иногда называют[12] законом смертности Гомперца – Мейкхема, но чаще просто законом Гомперца.
Ни Гомперц, ни Мейкхем не были биологами и не претендовали на открытие каких-либо механизмов старения. Они просто пытались описать статистические данные, оказавшиеся у них под рукой, чтобы предсказать вероятность, с которой тот или иной человек проживет долгую или короткую жизнь. Тем не менее выведенная ими зависимость продолжает соответствовать действительности и полтора века спустя. Какую бы страну в какой бы период времени мы ни взяли (если не учитывать войны и стихийные бедствия), графики смертности окажутся очень похожи на кривую Гомперца, особенно в середине жизни человека, на отрезке 20–70 лет. Поэтому самое распространенное среди геронтологов определение старения оказалось статистическим и звучит так: старение – это рост риска смерти от естественных причин.
Провал детства
Тем не менее кое в чем кривая Гомперца совсем не совпадает с реальностью. Расхождение между фактическими данными и моделью начинается сразу после рождения: похожий на параболу провал выравнивается и выходит на предсказанную кривую только после 20 лет.
Этому до сих пор не существует однозначного объяснения. Например, можно предположить, что дело в феномене "золотого детства". Минимальный риск смерти приходится на 9 лет, когда бытовые опасности уже отступили: ребенок достаточно самостоятелен, чтобы не упасть со стула или не опрокинуть на себя кастрюлю с кипятком, а подростковые – вроде самостоятельных прогулок по городу, вождения мотоцикла или уличных драк – еще не начались.
Можно подойти с другой стороны и поискать объяснение не провалу кривой в 9 лет, а ее подъему в самом начале жизни. Чем вызвана такая высокая младенческая смертность? Можно предположить, что это просто раннее действие естественного отбора: в утробе матери и в первое время после появления на свет гибнут те, кому достались неблагоприятные мутации в жизненно необходимых генах. По крайней мере, у мышей известно, что чем раньше[13] в ходе развития включается ген, тем сильнее на него действует естественный отбор. У людей может происходить то же самое – и тогда кривая смертности превращается[14] в сумму двух кривых: ранней смертности и возрастной смертности. В 9 лет первая уже минимальна, а вторая – еще минимальна, оттуда и видимый "провал".

Сам Гомперц в своей работе ничего не говорил о минимуме риска и "золотом детстве", и в его формуле нет ни единого на них намека. Возможно, дело в том, что страхового агента не интересовала детская смертность, а может, ему просто не хватило данных. Так или иначе, самым молодым из тех, кто попал в его статистическую выборку, было уже 10 лет.
Кроме того, провал на кривой на самом деле довольно неглубокий. Он становится заметен, только если специальным образом подобрать масштаб. Внимательный читатель, рассматривая график смертности современных людей, мог заметить, что он построен нелинейно. На оси Y риск умереть отложен по логарифмической шкале, то есть каждое крупное деление на ней соответствует не единицам, а порядкам величины (тысячные доли процента, десятые, единицы, десятки, сотни). Дело в том, что смертность возрастает очень резко, устремляется вверх гораздо круче, чем прямая линия. Если бы мы откладывали последовательно все тысячные доли процента риска в первые годы жизни, то на нашем графике не хватило бы места для десятков процентов во взрослом возрасте.
Такая логарифмическая шкала позволяет рассмотреть все изменения в подробностях. Как только мы переходим на привычную линейную шкалу, "провал детства" исчезает. Это значит, что, даже если бы Гомперц интересовался детской смертностью, он мог бы просто этого провала не заметить: по сравнению с тем, как сильно риск умереть растет у взрослых людей, его колебания в детстве кажутся несущественными.
Плато надежды
С другой, верхней, частью кривой Гомперца тоже не все оказалось гладко – в прямом смысле этого слова. Уже сам автор закона обнаружил (а впоследствии это подтвердили[15] и другие ученые), что его формула плохо описывает смертность после 75–80 лет. Реальный риск умереть во многих выборках оказывается ниже предсказанного: как в изначальных подсчетах Гомперца, так и во многих современных исследованиях. Например, в одной из недавних работ[16], авторы которой собирали статистические данные по долгожителям, кривая смертности и вовсе вышла на плато, то есть риски перестали расти после определенного возраста. Правда, это произошло лишь на 105-м году жизни. Поэтому даже если риск умереть действительно снижается, то людей, которые могли бы ощутить это на себе и своих сверстниках, среди нас очень мало.

Многим геронтологам этот факт кажется странным. Совершенно непонятно, что может произойти в организме человека в 105 лет (но не в 106 и не в 104), что вдруг повысило бы его шансы на выживание и тем самым, получается, остановило бы старение. Поэтому кривую смертности в позднем возрасте несколько раз пытались построить заново, другими методами и на других данных. Некоторым исследователям не удалось обнаружить[17] никакого снижения рисков, не говоря уже о выходе на плато, по крайней мере до 106 лет (а дальше уже сложно набрать достаточно данных). Откуда такое расхождение в результатах?
Первая причина – выборка людей, которая в каждом исследовании своя. В зависимости от ее размера и однородности (в идеале это должны быть люди одной национальности, с похожими датами рождения и жизненными историями) графики будут получаться разной формы. Если же в выборке оказались, например, половина граждан богатой и благополучной страны, а половина – бедной и терзаемой войнами, то итоговая зависимость не будет верна ни для тех, ни для других.
Вторая причина – искажения данных. Люди, которым сейчас больше 100 лет, родились в начале XX века, когда рождаемость и смертность не во всех странах строго фиксировались. Современные долгожители пережили несколько войн, иногда переезжали, у некоторых в связи с возрастом уже нарушена память, и они не могут снабдить исследователей точной информацией о себе. Кроме того, кто-то из них мог потерять документы во время войны или, наоборот, специально подделать их, чтобы его взяли в армию или сочли негодным к службе. И проверить истинность их даты рождения мы можем далеко не всегда.
Наконец, третья причина – недостаток людей, доживших до этого возраста. Чем меньше размер выборки, тем проще исказить статистику. Недавно австралийский исследователь Сол Ньюман подсчитал[18], что, если год рождения даже одного человека из 100 000 указан неверно, этого достаточно, чтобы создать на кривой Гомперца видимость плато. Если же таких ошибок будет 10 из 100 000, кривая и вовсе уйдет вниз, и получится, что в 110 лет люди рискуют умереть меньше, чем их 105-летние братья и сестры.
Тем не менее проблема плато старения не относится к принципиально нерешаемым (в отличие от поиска критериев старости). Базы данных расширяются, статистических исследований становится больше. Подрастает поколение долгожителей, родившихся после мировых войн в благополучных странах с четкой регистрацией рождаемости. По последним оценкам[19] Леонида и Натальи Гавриловых, которые занимаются демографией старения в США, чем свежее данные по долгожителям, тем они точнее укладываются в график Гомперца. Среди людей, родившихся в 1898 году, найти плато старения уже сложнее, чем среди тех, кто появился на свет в 1880 году, когда рождаемость фиксировалась хуже. Так что рано или поздно мы сможем точно подсчитать, снижается ли риск умереть после 105 лет, до этого времени нужно просто дожить.


