
Сен Гук Ким
Элементы
5. Специальное распределение натуральных чисел
1. Квадрат натуральных чётных чисел (2n)2 при n = 1; 2; 3; 4:
(2n)2 = 4; 16; 36; 64 (1)
2. Квадрат любого числа n равен сумме последовательных нечётных чисел:
n2 = Σ(2n –1) (2)
Это подтверждается последовательной подстановкой каждого из n = 1; 2; 3; 4:
Σ(2n –1) = 1; 1 + 3; 1 + 3 + 5; 1 + 3 + 5; 1 + 3 + 5 + 7
Тогда: (2n)2 = 2[2(1); 2(1 + 3); 2(1 + 3 + 5); 2(1 + 3 + 5 + 7)], (3)
и
(2n)2 = 2(2n2) = 2(2; 8; 18; 32) (4)
Получились числовые сдвоенности – Диады из числовых Монад: 2; 8; 18; 32.
Просуммируем все Диады (4) с учётом (2), (3) и правила: «от перестановки мест слагаемых сумма не изменяется».
Σ2(2n2) = 2Σ2Σ(2n –1) = 2{2[(1) + (1 + 3) + (1 + 3 + 5) + (1 + 3 + 5 + 7)]} = 2(2) + 2(2 + 6) + 2(2 + 6 + 10) + 2(2 + 6 + 10 + 14) = 2(2) + 2(6 + 2) + 2(10 + 6 + 2) + 2(14 + 10 + 6 + 2)
Полученный результат представляет полное количество KD чисел в четырёх Диадах из пар (2 перед скобками) Монад, которые состоят последовательно из 1, 2, 3, 4 слагаемых (в скобках). В сумме они составляют:
KD = 2(2) + 2(6 + 2) + 2(10 + 6 + 2) + 2(14 + 10 + 6 + 2) = 120 (5)
С учётом (3) формулу (4) можно записать как последовательность количества KN номеров N в Монадах последовательности n = 1; 2; 3; 4 Диад:
KN = 2(2n2) = 2Σ2(2n –1) = 2[2(1), 2(3 + 1), 2(5 + 3 + 1), 2(7 + 5 + 3 + 1)] (6)
Произведя суммирование и раскрытие скобок в правой части формулы (6), получим распределение количества KN номеров N в n = 1; 2; 3; 4 Диадах:
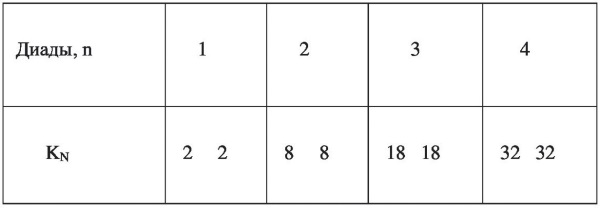
Это именно количества номеров, которые не обязательно должны следовать по определённому нарастающему порядку в монадах. Номера же должны последовательно нарастать. Номера N, в отличие от KN по формуле (6), должны выстраиваться в последовательных монадах 1–4 Диад по этой же простой формуле:
N = 2Σ2(2n –1), (7)
но в последовательно нарастающем порядке от 1 до 120.
Все значения KN чётные. Поэтому можно построить геометрическое воплощение формул (5) и (6) в виде вертикально-симметричной последовательности 20-ти рядов ячеек-квадратиков 8-ми Монад для 1-120 номеров N в n = 1; 2; 3; 4 Диадах-Уровнях сверху вниз:

Рис. 10. Вертикально-симметричное 4-Уровневое распределение ячеек-квадратиков для 1-120 номеров в 20-ти рядах 8-ми Монад по формуле (6)
Ряды 1, 2,4, 6, 9,12,16, 20 состоят из 2 ячеек, ряды 3, 5, 8, 11, 15, 19 – из 6 ячеек, ряды 7,10, 14, 18 – из 10 ячеек, ряды 13, 17 – из 14 ячеек. В целом форма с ячейками напоминает ветвистую Ёлку. Ряды с двумя ячейками выглядят стволом Ёлки. Очевидно, ствол отличается от ветвей. И первые ветви Уровней n = 2; 3; 4 отличаются друг от друга. Таким образом, Ёлка составлена из ствола и трёх разных ветвей. Эти очевидные различия отразим тонами серой шкалы (gray scale).
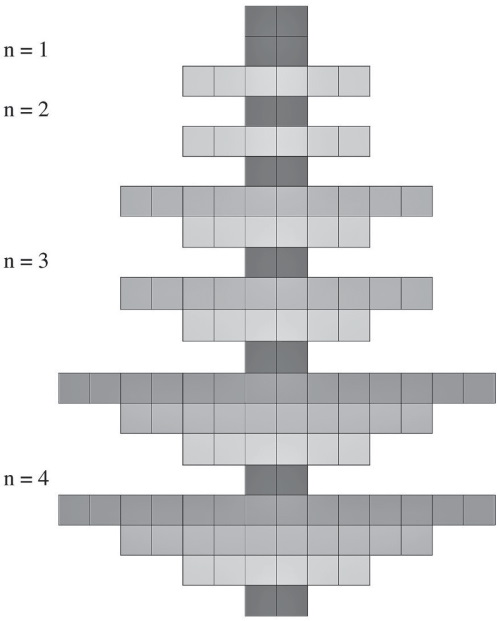
Рис. 11. Ячейки Ёлки в различных тонах серой шкалы
Первый ряд первой диады из двух ячеек задаёт однообразие стволовых ячеек первого типа в остальных нижележащих подобных семи рядах. Третий ряд (первый ряд во второй Диаде) задаёт шестиячеечный первый тип ветви Ёлки в нижележащих подобных пяти рядах. Седьмой ряд (первый ряд в третьей Диаде) задаёт десятиячеечный второй тип ветви Ёлки в нижележащих трёх подобных рядах. Тринадцатый ряд (первый ряд в четвёртой Диаде) задаёт четырнадцатиячеечный третий тип ветви Ёлки в нижележащем одном ряду. Таким образом, первые ряды с 2, 6,10,14 ячейками являются типозадающими для нижележащих подобных рядов, и все 120 ячеек закономерно подразделяются на 4 типа.
Пронумеруем ячейки последовательно в строго нарастающем порядке слева направо в рядах с последовательным переходом на нижележащие ряды сверху вниз. При этом номера n = 1, 2, 3, 4 Диад-Уровней и рядов 1-20, зафиксированные на рис. 10 и номера Диад-Уровней на рис. 11, опустим.

Рис. 12. Последовательная нумерация ячеек на рис. 11
В соответствии с разделением ячеек на четыре типа и последовательные номера 1-120 распределяется по этим четырём типам.
6. Преобразование формы Ёлки
Форма Ёлки на рис. 12 монотонна, 4 уровня выражены не чётко. Имеет смысл перейти к другой форме – Ёлке 1. Преобразование Ёлки к Ёлке 1 проводится последовательными перестановками наверх рядов нижних монад Диад на уровнях 2, 3 и 4, не нарушающими правило: от перестановки мест слагаемых (рядов) сумма не изменяется. Очевидно, преобразование должно быть обратимым:
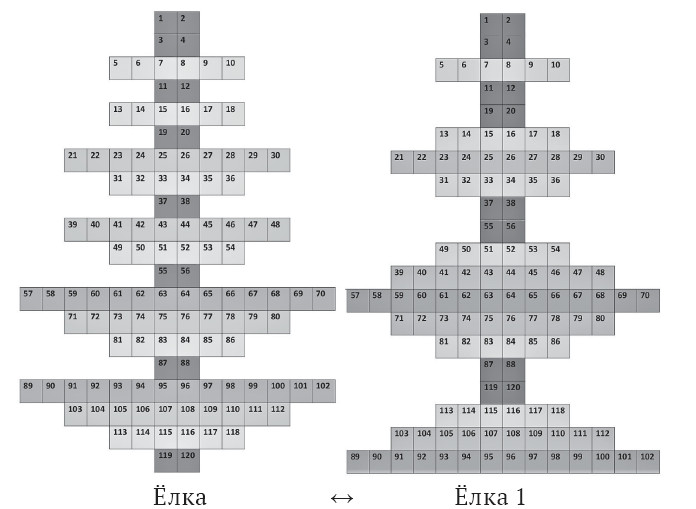
Рис. 13. Преобразование Ёлки в Ёлку 1
Повернём Ёлку 1 на 90° против часовой стрелки в горизонтальное положение:

Рис. 14. Горизонтальное положение Ёлки 1.
Диады-Уровни 1, 2, 3,4 имеют конфигурации с последовательным наращиванием квадратиков от Квадрата из 4-х квадратиков до Прямоугольника 8 × 14 с симметричными ступенчатыми выемками.
Разнесём верхние и нижние части Диад-Уровней Ёлки 1 по горизонтальной оси симметрии так, чтобы из них образовалась непрерывная последовательность верхних и нижних половин Диад-Уровней:

Рис. 15. Последовательность верхних и нижних половин Диад-Уровней Ёлки 1 на рис. 14
Полученная картина напоминает «волну из симметричных половин Диад-Уровней. Они изменяются и по ширине, и по высоте на два квадратика. Такую «импульсную последовательность» распределения чисел-номеров нельзя называть периодической, потому что промежутки между импульсами (периоды) не постоянны. Но с учётом того, что ширина и размах импульсов последовательно увеличиваются на постоянное число 2, т. е. по арифметической прогрессии, полученную закономерность можно называть прогрессионно-периодической или кратко – про-периодической.
7. Свёртка ветвистой Ёлки 1 в компактную форму
Первая Диада в Ёлке 1 на рис. 13 уже в компактной форме Квадрата 2 × 2 из 4-х квадратиков с номерами: 1,2,3,4. Квадраты 2 × 2 можно рассматривать как квадратные слои первого типа, окаймляющие внутренний Квадрат со стороной, равной 0. Квадраты с квадратиками будем писать с прописной буквы К.
Во второй Диаде Ёлки 1 ячейки с номерами 5, 10 и 13, 16 переместим так, чтобы образовался второй тип Квадратного слоя из 12 ячеек, окаймляющий первый тип Квадратного слоя из ячеек с номерами: 11,12 и 19,20.
В третьей Диаде ячейки с номерами 31,36 и 49,54 переместим так, чтобы образовался второй тип Квадратного слоя из 12 ячеек, окаймляющий первый тип Квадратный слоя из ячеек с номерами: 37, 38 и 55, 56. Ячейки с номерами 21, 22, 23, 28, 29, 30 и ячейки с номерами 39, 40, 41, 46,47,48 переместим так, чтобы образовался третий тип Квадратного слоя из 20 квадратиков, окаймляющий второй тип Квадратного слоя.
В четвёртой Диаде ячейки с номерами 81, 86 и 113, 118 переместим так, чтобы образовался второй тип Квадратного слоя, окаймляющий первый тип Квадратного слоя из ячеек с номерами 87, 88, 119, 120.
Ячейки с номерами 71, 72,73 и 103, 104, 105 переместим так, чтобы образовался третий тип Квадратного слоя из 20 ячеек, окаймляющий второй тип Квадратного слоя. Ячейки с номерами 57–60, 67–70 и 89–92, 99-102 переместим так, чтобы образовался четвёртый тип Квадратного слоя с верхними номерами 57–70, и нижними номерами 89-102 из 28 ячеек, окаймляющий третий тип Квадратного слоя.
В результате этих перемещений получим свёртку разветвлённой Ёлки в компактную фигуру из Квадратов 2 × 2, 4 × 4, 6 × 6 и 8 × 8, напоминающую Монумент.

Рис. 16. Монумент из 1-120 ячеек в Квадратах 2 × 2, 4 × 4, 6 × 6, 8 × 8
Типизация пронумерованных ячеек тонами серой шкалы на рис. 11 сохранилась, но не в линейных рядах, а в концентрически замкнутых Квадратных слоях.
8. «Волновое» распределение чисел-номеров в половинах Квадратов
Вертикальную последовательность Квадратов 2 × 2, 4 × 4, 6 × 6, 8 × 8 сверху вниз на рис. 16 в уменьшенном масштабе переведём на горизонтальную их последовательность слева направо:
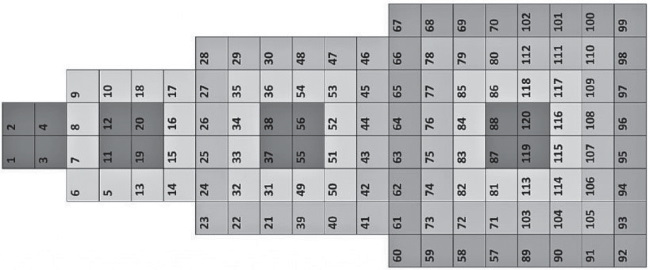
Рис. 17. Горизонтальная последовательность Квадратов 2 × 2, 4 × 4, 6 × 6, 8 × 8
Разнесём верхние и нижние половины Квадратов 2 × 2, 4 × 4, 6 × 6, 8 × 8 на рис. 17 в непрерывную последовательность вдоль срединной горизонтальной линии:

Рис. 18. Непрерывная последовательность половин Квадратов 2 × 2, 4 × 4, 6 × 6, 8 × 8 Уровней 1, 2, 3, 4
Получилась последовательность «волн прямоугольных импульсов» с нарастанием аргумента на 4 единицы, а амплитуды на 1 единицу с каждой последующей «волной». Нет определяющего признака периодичности – постоянства периода. Поэтому такая последовательность не является периодической в строгом определении понятия периодичности. Но, поскольку аргумент и амплитуда изменяются на постоянные числа в арифметической прогрессии от «импульса» к «импульсу», то полученную закономерность можно называть прогрессионно-периодической (про-периодической).
Таким образом, и для случая Диадной (Ёлочной), и для случая Квадратной (Монументальной) форм распределения натуральных чисел-номеров получается прогрессионно-периодическая (про-периодическая) закономерность в последовательности их распределения.
Ёлочное Диадное (рис. 12, 13.) и Монументальное Квадратное (рис. 16) распределения пронумерованных ячеек исключительно математического (теоретического) происхождения. Они могут быть эффективны для разных множеств объектов реального Мира, как искусственных, так и естественных. Например, в искусственных построениях таким может быть эффективный ступенчато-клинообразный строй бойцов, подразделений, боевых машин, танков, судов, самолётов, воинских соединений для прорыва оборонительных линий или наступательного фронта противника. Для естественных объектов можно сопоставить их с распределением множества химических элементов.
9. Распределения множества химических элементов
На рис. 12 и на рис. 16 ячейки с номерами дополним символами соответствующих химических элементов. Все существующие на сегодня химические элементы отнесены к 4-м блокам: s, р, d, f. Ячейки с химическими элементами этих блоков обычно отцвечивают соответственно красным, жёлто-оранжевым, синим и зелёным цветами. На нижеследующих рис. 19 и рис. 20 представлены числовая Ёлка на рис. 12 и Числовой Монумент на рис. 16 с символами химических элементов и в цветах ячеек s, р, d, f блоков. По логике формул (5) и (6) элементы 119 и 120 должны быть s-элементами. Но они ещё не обнаружены и не синтезированы. Ячейки с этими элементами отцвечены не красным, а тёмно-красным цветом.

Рис. 19. Ёлка химических элементов
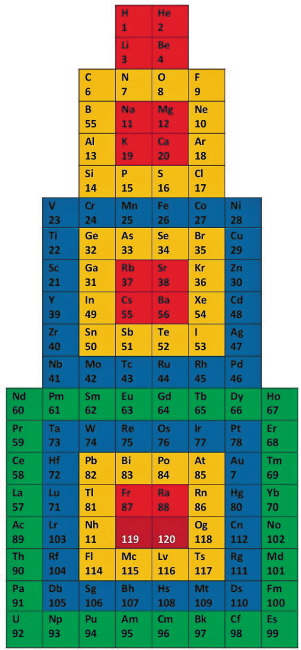
Рис. 20.Монумент химических элементов
Разделы 5 и 7 завершились выявлением четырёх типов ячеек, которые были зафиксированы различными тонами серой шкалы. Рассмотрим совместно Числовую Ёлку (рис. 12), числовой Монумент (рис. 16), Ёлку химических элементов (рис. 19) и Монумент химических элементов (рис. 20).

Рис. 21. Совместное представление рис. 12, рис. 19 и рис. 16, рис. 20
В Ёлочном распределении химических элементов первая пара s-элементов первого уровня проявляет свою типозадающую роль тем, что все пары «стволовых» элементов являются «красными» s-элементами. В Монументе химических элементов этот тип проявляется «красными» квадратиками в четырёх концентрических слоях из четырёх ячеек в Квадратах 2 × 2, 4 × 4, 6 × 6, 8 × 8.
Первая оранжевая «ветвь» второго уровня Ёлки химических элементов задаёт тип остальных р-элементов. В Монументе все p-элементы располагаются во вторых концентрических слоях, окаймляющих Квадраты из двух пар s-элементов.
Первая «синяя ветвь» третьего уровня Ёлки химических элементов задаёт тип остальных ветвей d-элементов. В Монументе все d-элементы располагаются в третьих концентрических слоях, окаймляющих вторые концентрические слои р-элементов.
Первая зелёная «ветвь» четвёртого уровня Ёлки химических элементов задаёт тип остальных 14-ти f-элементов. В Монументе все f-элементы располагаются в четвёртом концентрическом слое, окаймляющем третий концентрический слой из d-элементов.
Сравнение фигур 1 с 2 и 3 с 4 на рис. 21 показывает совпадение типизации ячеек тонами серой шкалы и ячеек с цветами s, р, d, f блоков. Поскольку Систематизация и типизация ячеек с номерами 1-120 на фигурах 1 и 3 тонами серой шкалы были проведены исключительно математически, то и фигуры 2 и 4 представляют математическую Систематизацию и Типизацию химических элементов. Математическая типизация совпадает с квантово-механической типизацией s, р, d, f – блоками.
Совпадение квантово-механической типизации химических элементов и их типизации на основе закономерностей распределения натуральных чисел в квадратах чётных чисел удивительно, даже поразительно. Ведь, что получается? Натуральные числа, чётные числа, нечётные числа известны человечеству тысячелетия. Это только человечеству. В природе, во Вселенной они всегда были. Химические же элементы начали открывать лишь в XVIII веке. А числа уже «знали» о четырёх типах химических элементов (!).
10.4-Уровневая Диадная Таблица химических элементов
Ячейки на рис. 19 последовательны, но с большим количеством «пустот» между Монадами и Диадами. Уплотнением фигуры, т. е. сокращением количества «пустот» между Монадами и Диадами, далее, расширением квадратиков до прямоугольников для возможности размещения в них дополнительной информации (атомные массы, электронную структуру, числа нуклонов….), наконец, размещением в рамки с номерами Уровней и Групп, можно получить 4-Уровневую Диадную Таблицу химических элементов:

Рис. 22. 4-Уровневая Диадная Таблица химических элементов
Наверху Таблицы помещены три симметричные полосы с номерами групп в ячейках s-, р-, d-, f-расцветок, в точности соответствующие цветам ячеек в рядах этих элементов. Групп XXXII, но столбцов всего 14. У Периодической Таблицы IUPAC XVIII групп и 18 столбцов. Номера групп в цветных ячейках трёх полос в точности указывают на элементы-аналоги по всем столбцам Таблицы. Слева сбоку указаны номера Уровней (Диад). Их только 4. Каждый Уровень состоит из двух количественно равных половин. Они в Периодической Таблице IUPAC представляются Периодами. Все элементы располагаются
в одной Таблице без внутренних пустых ячеек, тогда как в Таблице IUPAC 36 внутренних пустых ячеек наверху основной таблицы, а лантаноиды и актиноиды вынесены в отдельные дополнительные таблицы. Это основательные нарушения принципа непрерывности-целостности в последовательности химических элементов, заложенного Д.И. Менделеевым в качестве главного принципа Систематизации химических элементов.
11. 4-Уровневая Диадно-октавная Таблица химических элементов
Несмотря на то, что IUPAC с 1989 г. рекомендует длиннопериодную XVIII групповую Таблицу химических элементов, подавляющее большинство образованных людей и специалистов «сохраняют верность» короткопериодной октавной Таблице химических элементов. Она на самом деле удобнее для образовательного, научного и практического пользования. В учебной, научной и технической литературе давно утвердились и укоренились термины: соединения АIIBYI, АIIIBY, …, двойные системы АII – BYI, АIII – BY, …, которые возникли в период широкого пользования короткопериодной октавной Таблицей Менделеева.
Перестановками ячеек d и f элементов на рис. 22 без нарушения их непрерывной последовательности в рядах можно получить 4-Уровневую Диадно-октавную Таблицу химических элементов (рис. 23). Получается довольно много пустых ячеек. Но все они внешние по отношению к рядам с ячейками химических элементов и не нарушают принципа непрерывности-целостностности. В короткопериодной же Таблице Менделеева и в XVIII-ти групповой Периодической Таблице IUPAC пустые ячейки внутренние и они нарушают принцип непрерывности в элементных последовательностях.
Наверху Таблицы помещена 5-рядная схема последовательности номеров групп в ячейках расцветок s, р, d, f блоков химических элементов. Эти номера относятся только к соответствующим цветам ячеек химических элементов, например, к красным группам I и II относятся только химические элементы в красных ячейках сверху вниз, а к зелёным группам XIX–XXXII имеют отношение по вертикалям только соответствующие лантаноиды и актиноиды. Медь с благородными металлами и группа Цинка оказались в одних столбцах с группами I и II, что ещё больше сближает эту Таблицу с короткопериодной VIII-групповой Таблицей Менделеева.

Рис. 23. 4-Уровневая Диадно-октавная Таблица химических элементов


