
Тимур Машнин
Объектно-ориентированное программирование на Java. Платформа Java SE
Представление данных и типы данных

Давайте посмотрим под капот калькулятора или компьютера, и посмотрим, как мы можем представлять данные.
И начнем с простого.
Давайте посмотрим на логические значения, потому что там есть только два значения, true и false.
Цифровые компьютеры состоят из электроники, которая может находиться только в одном из двух состояний.
Триггер – это базовая единица, которая может оставаться либо в одном положении, либо в другом.
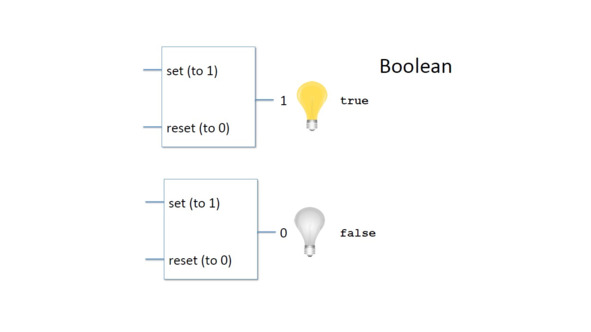
Выход триггера остается в одном из этих двух состояний и будет оставаться там до тех пор, пока не появится сигнал для его изменения.
В действительности 1 может иметь нулевое напряжение, а другое состояние – пять вольт.
Но мы можем произвольно интерпретировать их как 0 и 1.
Поэтому мы можем сказать, что триггер может хранить один бит информации.
Теперь это именно то, что нам нужно, чтобы сохранить логическое значение, потому что логических значений также два, ложь и истина.
И мы, опять же, можем произвольно присвоить 0 false и 1 true.
Итак, мы говорим, что нам нужен бит, чтобы сохранить логическое значение.
Теперь, если у вас есть два триггера, мы можем сохранить два бита.
Если мы соберем их вместе, у нас будет четыре возможных комбинации: 0—0, 0—1, 1—0 и 1—1, поскольку каждый из них может иметь состояние 0 или 1 независимо друг от друга.
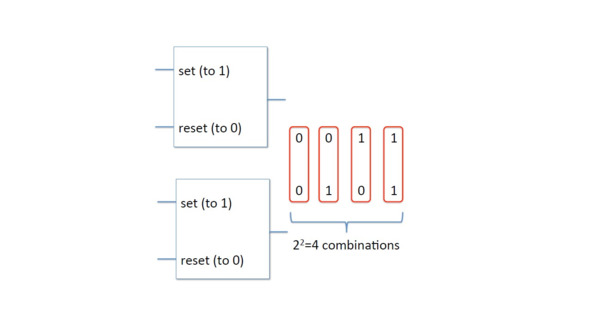
И если мы возьмем восемь триггеров, чтобы сохранить восемь бит, у нас будет 2 в степени 8 различных комбинаций.
То есть 256 комбинаций в целом.

Что мы можем с ними делать?
Восемь бит называется байт.
Итак, что мы можем сделать с байтом?
Мы можем представить 256 различных чисел.
Например, натуральные числа от 0 до 255.
Мы также можем отображать 256 уровней красного, от черного до ярко-красного.
И мы можем получить любой цвет, составляя уровни красного, зеленого и синего.
Для каждого из этих компонентов мы используем один байт.
Таким образом, это всего три байта или 24 бита, что означает 2 в степени 24, что почти 17 миллионов цветовых комбинаций.
Звуки, фильмы, все представлено битами 0 и 1.
Это позволяет нам иметь богатую информацию, но в тоже время иметь единый способ обработки этой информации.
Наконец, мы можем также представлять отдельные символы, как те, которые есть у вас на клавиатуре, а также некоторые другие специальные символы.
Для этого существует множество кодировок.
Java использует кодировку юникода, использующую 16 бит.
Другие кодировки используют только восемь бит.
Таким образом, все в компьютере представлено битами.
Все сводится к нулям и единицам.
Давайте сосредоточимся на том, как мы представляем числа в двоичной форме битами.
С 1 байтом – 8 бит – мы можем сформировать 256 различных комбинаций, или 2 в степени 8.

Поэтому мы можем представить 256 различных чисел.
Это могут быть, например, натуральные числа от 0 до 255.
Но какая комбинация байт соответствует какому числу?
Давайте проанализируем систему, которую мы используем для представления чисел в нашей десятичной системе, которая использует 10 цифр, от 0 до 9.
Используем систему, основанную на весах.
Чем больше мы двигаемся влево, тем выше вес.

Когда мы пишем 972, мы имеем в виду 9 умножить на 100 плюс 7 умножить на 10 плюс 2.
Так как здесь основание 10, система исчисления называется десятичной.
Для двоичной системы исчисления тот же принцип, только основанием будет 2.
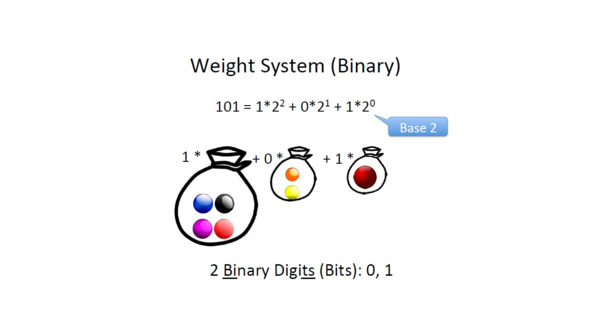
Соответственно, перевести число из двоичной системы в десятичную очень просто, нужно сложить получившийся ряд.

Перевести число из десятичной системы в двоичную тоже просто, нужно делить на 2 и записывать остаток.

Но как насчет отрицательных чисел? Нам тоже нужно работать с ними.
Неотрицательные числа, т. е. 0 и положительные числа – закодированы по-прежнему, где самый левый бит установлен в 0.

И у нас осталось семь бит.
Таким образом, мы можем иметь 2 в степени 7 различных неотрицательных чисел, а именно от 0 до 127.
Для отрицательных чисел они кодируются таким образом, что сумма отрицательного числа и его положительного аналога равна 2 в степени числа бит, т. е. восемь, или 256, или 1, а затем восемь 0.
Таким образом, с этим кодированием мы можем представлять, как положительные, так и отрицательные числа.
Теперь давайте сосредоточимся на Java.
Какие типы данных мы используем для целых чисел?
На самом деле это не один тип данных, а доступно несколько типов данных.

У нас есть тип данных, называемый «байт», который использует точно восемь бит – это и есть, один байт.
Мы можем представить цифры от -128 до 127, как мы только что видели.
Есть тип данных «short», который использует 16 бит и находится в диапазоне от -32 000 до плюс
32000.
Но основным типом данных, которым мы будем пользоваться, будет «int».
Здесь максимальное положительное число составляет более 2 миллиардов.
Если вам потребуются большие цифры, можно использовать «long» с 64 битами.
Для чисел с плавающей запятой есть два типа данных в Java: «float», который использует 32 бита, и «double», который использует 64 бита.

Рекомендуется использовать double, когда нужны числа с плавающей запятой.
Подводя итог, существует восемь примитивных типов данных в Java.
Два для представления нечисловых данных: boolean для булевых значений, true и false, и char – для представления одного символа.

И числовые типы данных.
int – это основной тип данных, который нужно запомнить для представления целых чисел.
И остальные байт, short, и long.
И double – это основной тип данных для чисел с плавающей запятой.
Другой тип – float.
Таким образом мы не можем работать с бесконечно большими числами или числами с бесконечной точностью.
Методы

Представьте себе, что вам приходится многократно вычислять квадрат числа.
Для каждого числа, вы вводите одно число, затем оператор умножения, а затем снова число.
И то же самое для другого числа и т. д.
Поэтому в калькуляторе было бы неплохо иметь программируемую кнопку, которая выполняет любую операцию, которую мы определим.
Это может быть квадрат или квадратный корень, или любые вычисления, которые нам понадобятся.

В Java также возможно определять пользовательские операции.
Но вместо того, чтобы называть их операциями, мы называем их методами.
Это является терминологией Java.
В других языках программирования они называются функциями или процедурами.
Метод – это вычисление, которому мы даем имя, так что мы можем вызывать его в любое время, когда нам нужно выполнить это вычисление.
Метод может зависеть от одного или любого числа параметров.
И метод может привести к какому-то результату или какому-то эффекту.
Рассмотрим метод вычисления квадрата числа.
Можно представить этот метод как черный ящик, который получает целое число в качестве входных данных и выводит другое целое число.
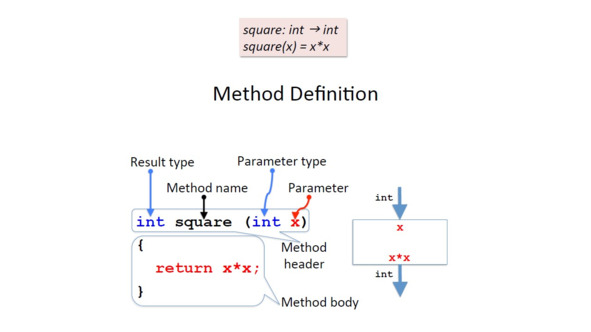
В математических терминах мы можем определить его как функцию следующим образом.
Мы дадим функции имя, например, square.
И эта функция принимает целое число как параметр и возвращает целое число.
Функция определяется следующим образом.
Если мы назовем аргумент или параметр как x, результат получается умножением x на x.
Теперь, как мы определим это в Java?
Сначала мы напишем что-то похожее на первую строку в математическом определении.
Но порядок немного другой.
Во-первых, мы пишем тип результата, затем имя метода, а затем в круглых скобках тип параметра и далее идентификатор параметра.
При этом у нас может быть несколько параметров.
Все это называется заголовком метода.
Затем мы напишем в фигурных скобках то, что мы должны сделать, чтобы вычислить результат.
И мы указываем, что это результат возврата, поместив ключевое слово return перед выражением.
Затем в фигурных скобках мы пишем вычисление, которое хотим выполнить.
И мы называем это телом метода.
Имя метода может быть любым допустимым идентификатором.
Но мы будем следовать соглашению, и напишем его с маленькой буквы.
И обычно это глагол.
Если нам нужно больше одного слова, мы будем писать каждое следующее слово с заглавной буквы.

Как мы видим здесь в isEmpty.
И рекомендуется, чтобы имя метода имело значение, чтобы другие могли легко понять, что здесь вычисляется.
Имена параметров мы также можем свободно выбирать.
Нам нужно дать имя параметру, потому что нам нужно обращаться к параметру в теле метода.
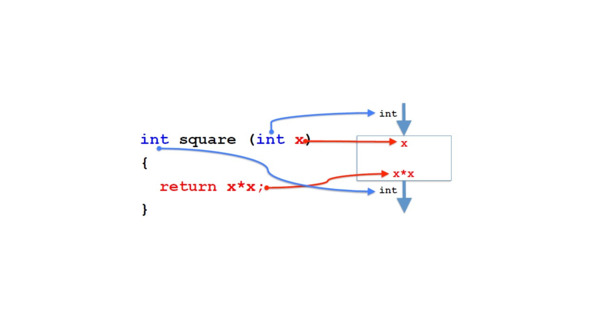
Но этот идентификатор является внутренним.
Если мы заменим его на другой идентификатор, мы не изменим метод.
Вместо x мы можем указать y в качестве идентификатора параметра.
Так как, по существу, x или y являются просто заполнителями для фактического параметра, который мы указываем при вызове метода.
Сколько входных параметров может иметь метод?
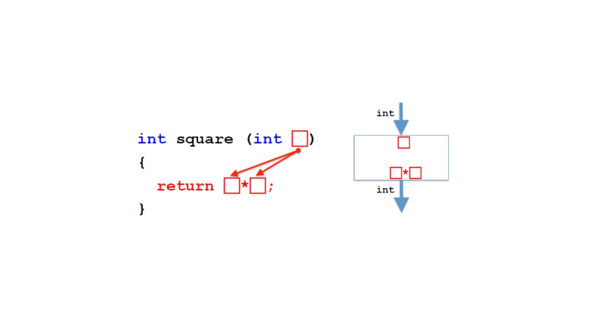
И что насчет результата?
Мы видели, как определить метод с одним параметром и одним результатом.
Можем ли мы также иметь больше параметров?
У нас может быть несколько параметров.
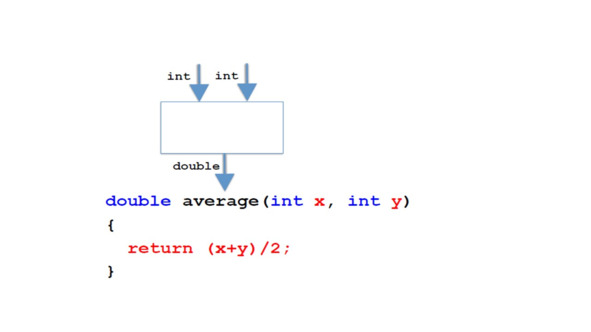
Здесь мы видим метод с двумя параметрами.
Обратите внимание, что они разделяются запятыми.
И у нас может быть еще больше параметров, разделенных запятыми.
Также у нас может не быть никаких параметров.
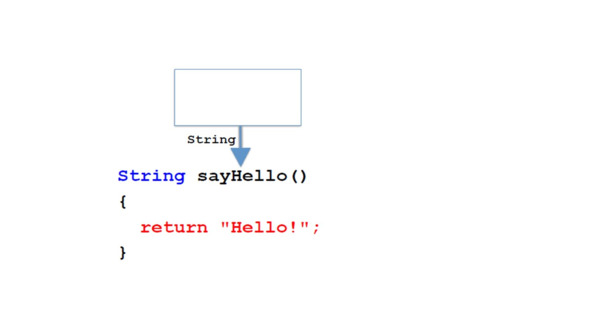
Теперь круглые скобки пустые.
В этом случае этот метод всегда возвращает одно и то же значение.
Или у нас может не быть никакого возвращаемого результата.

В этом случае мы пишем void как тип результата.
Это имеет смысл, например, если мы хотим что-то напечатать.
В других языках программирования говорят о процедурах, если нет возвращаемого значения.
И о функциях, если возвращается результат.
Но в Java мы просто говорим о методах.
Наконец, мы можем иметь метод без параметров и без результатов.

Теперь мы рассмотрели все возможные случаи.
Область видимости переменных

В предыдущей лекции мы узнали, как определить метод.
И мы хотим знать, что происходит, когда мы его вызываем.
Возьмем снова метод, вычисляющий квадрат числа.
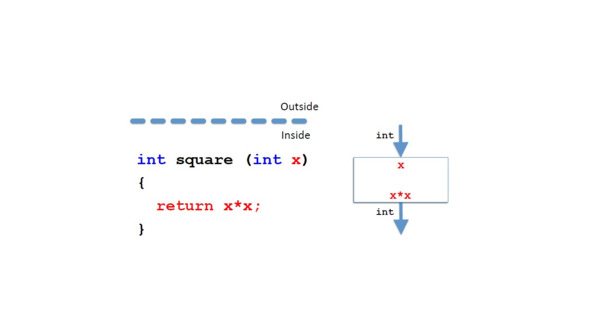
Он называется square и принимает одно значение и возвращает другое значение – квадрат числа.
Важно отметить, что определение метода идентифицирует два контекста – внутри и снаружи.
Внутри мы можем использовать параметры x или y или что угодно.
Но не снаружи.
Извне мы просто знаем название метода, параметры, и тип результата.
Как вычисляется метод, это вопрос внутреннего контекста.
В какой-то момент мы могли бы изменить тело метода.
Здесь мы видим альтернативный способ вычисления квадрата числа.
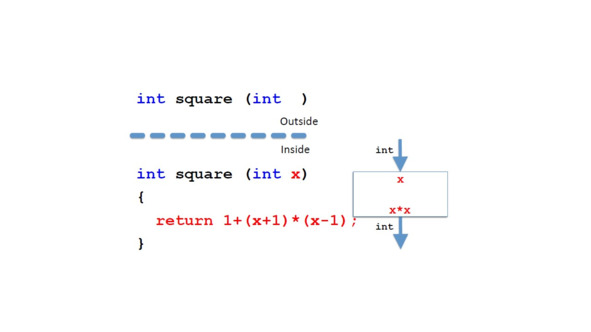
Но мы не знали бы этого извне, из контекста вызова.
Теперь давайте посмотрим, что происходит, когда мы вызываем метод с заданным значением.
Мы могли бы проанализировать, что происходит, когда мы вызываем square (3).
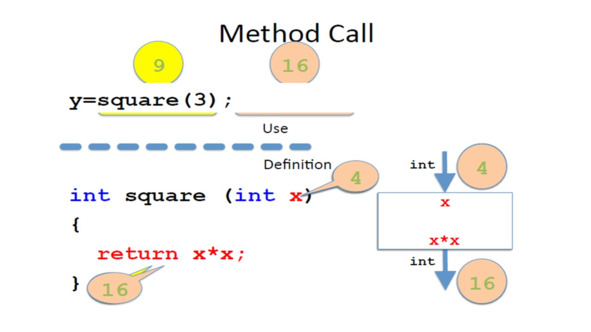
Но давайте сделаем немного интереснее.
Попробуем оценить выражение square (3) + square (4).
Чтобы получить результат суммы, сначала мы должны вычислить первый операнд, square (3).
И для этого мы перейдем к определению метода, где x теперь равно 3.
Это означает, что мы должны заменить все x на 3.
Таким образом, мы вычисляем 3 умножить на 3.
Результат будет – 9, и это то, что возвращает вызов метода.
9 теперь является значением первого операнда суммы.
Затем нам нужно вычислить значение для square (4).
Перейдем к определению метода, но теперь x равно 4.
3 больше не существует.
Поэтому мы заменяем все x на 4, и поэтому умножаем 4 на 4.
Этот вызов метода возвращает 16 вызывающему выражению.
Теперь у нас есть оба операнда, и мы можем сложить 9 и 16.
Во всех этих вычислениях важно отметить, что два вызова одного и того же метода полностью независимы.
Мы использовали x с двумя независимыми значениями.
Сначала 3, а затем 4.
И когда мы использовали 4, 3 уже не существовало.
Каждый раз, когда мы делаем новый вызов, параметры создаются со значениями вызова.
Значения, которые мы имели от предыдущих вызовов, просто забываются.
Мы использовали идентификаторы или имена в разных целях: для переменных, для методов, для параметров метода и т. д.
Теперь возникает вопрос: если у нас есть переменная с именем «x», а затем у нас есть метод с параметром.
Можно ли назвать этот параметр как «х»?
Или будет какая-то несовместимость?
Можем ли мы использовать одно и то же имя в разных контекстах?
Давайте рассмотрим пример.
Представьте, что у нас есть программа, где есть целочисленная переменная с именем x,

Которую мы инициализируем в значение 1.
И у нас также есть метод «f», который имеет целочисленный параметр.
И мы просто решили назвать его «х».
Вопрос, можем ли мы это сделать?
И если да, то что этот метод вернет в качестве результата?
Ответ на этот вопрос при написании кода на Java – да, мы можем это сделать.
Каким образом, мы управляем двумя x?
Каждый x действителен в определенном контексте, при выполнении определенного сегмента кода.
У нас есть черный x, который действителен, и который существует, и для которого мы сохраняем пространство в памяти, когда объявляем переменную.
Мы также зарезервировали пространство в памяти для z.
И когда мы вызываем f с x плюс 1, значение x равно 1.
1 плюс 1 равно 2, и мы вызываем f с 2.
Далее мы переходим к определению метода.
Вызываем f с 2.
Таким образом, красный x равен 2.
Итак, мы выполняем x плюс x со значением 2.
2 плюс 2 равно 4.
И это то, что этот метод возвращает и что хранится в z.
Теперь помните, что параметр x метода f является просто заполнителем.
Поэтому, если f вызывается с переменной x, а значение x равно 2, f с x возвращает 4.
И с этим нет никаких проблем.
Мы говорим, что первое x является глобальной переменной, тогда как параметр x является локальным для метода.
В этом примере мы видим, что эта локальная переменная – этот параметр – создается дважды: во-первых, для внутреннего вызова f с x плюс 1, со значением 2, – и второй раз для внешнего вызова со значением 4.

После выхода из каждого определения метода, созданная переменная будет уничтожена.
И выделенное пространство в памяти компьютера будет освобождено.
Поэтому, если вы хотите использовать внешнюю переменную в теле метода, вы должны выбрать другое имя.
Здесь мы видим, как использовать глобальную переменную x и параметр y в теле метода.

В этом случае у нас есть переменная x, которая видна во всем теле метода и за его пределами, и у нас есть переменная y, которая существует и видна только в теле метода.
Вне этого метода y не существует.
В этом примере, все, что мы только что сказали для параметров метода, применяется к переменным, объявленным внутри тела метода.

Здесь переменная y является локальной переменной в методе f.
В этом методе мы используем глобальную переменную x и локальную переменную y.
Этот пример аналогичен предыдущему.
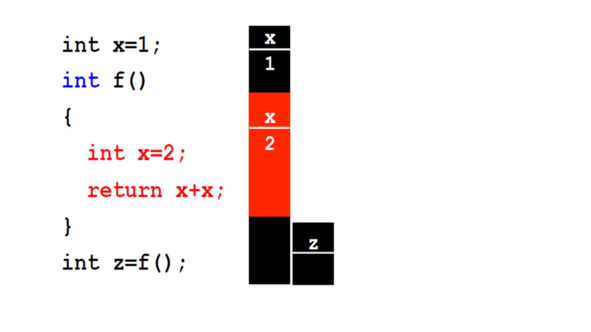
Но в этом случае мы решили назвать локальную переменную внутри метода x, так же, как и глобальную переменную.
Таким образом, в этом случае у нас нет доступа к глобальной переменной.
Когда мы вызываем f для вычисления z, мы вызываем f, где внутри определяется x со значением 2.
Таким образом, мы возвращаем 2 плюс 2, равно 4.
Метод f всегда возвращает 4.
И это то, что мы сохраним в переменной z.
Таким образом, мы видели, что у нас есть глобальные и локальные переменные.
Глобальные переменные существуют, начиная с объявления и для остальной части программы.
Но они могут временно затеняться другими локальными переменными с тем же именем.
В этом примере показан цикл.
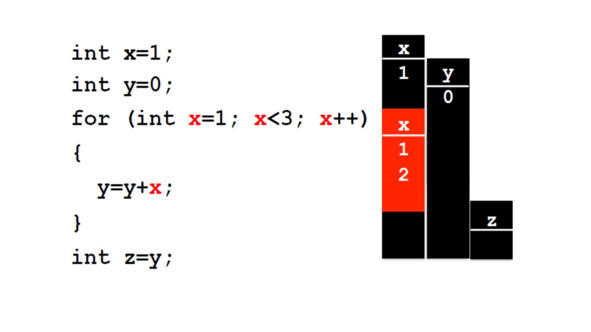
Для циклов также объявляются локальные переменные.
Здесь переменная x цикла for не позволяет нам видеть глобальную переменную при выполнении цикла.
Здесь у нас есть глобальная переменная x и глобальная переменная y.
Они инициализируются 1 и 0 соответственно.
Затем у нас есть глобальная переменная z, которая сохраняет значение y, но после выполнения этого цикла for.
Этот цикл for выполняется дважды.
Один раз для x равного 1 и один раз для x равного 2.
В каждом цикле for, y накапливает значение x.
Таким образом, при первом запуске y получает значение 1, а во втором y получает значение 1 плюс 2, равно 3.
Когда мы выходим из цикла for, локальная переменная x исчезает, остается только глобальная.
y имеет значение 3, и это значение, которое мы сохраняем в z.
Таким образом, мы видим точно такое же поведение для этих переменных в цикле for, как мы видели с локальными переменными в методах и с параметрами в методах.
В этом примере у нас есть глобальная переменная x.

И у нас есть метод с параметром x.
И внутри этого метода у нас есть цикл for с другой переменной x.
Таким образом, в этом случае у нас есть 3 переменных x.
Поэтому, когда мы вызываем f с x плюс 2, в последней строке, где x равно 1, мы вызываем f с 3, чтобы вычислить z.
В методе, параметр x равен 3.
Внутри метода мы объявляем переменную y, инициализированную 0, и затем мы определяем цикл for.
Этот цикл for выполняется два раза, как в предыдущем примере.
Здесь, мы объявляем другую переменную x, которая делает невидимыми предыдущие две переменные x, пока мы не выполним цикл for.
Здесь мы увеличиваем значение y.
y в конце получает 3 и возвращает y плюс x.
Но что это за х?
Это не та переменная x в цикле for, потому что мы вышли из цикла for.
Эта x равна 3 и это параметр метода.
Поэтому возвращается 3 плюс 3.
Это то, что мы возвращаем z, и что добавляется к x, но в этом случае это глобальная переменная x, поэтому мы получаем 7 и присваиваем 7 в z.
Этот пример легко проанализировать.

Метод f определяется в контексте, где x равно 1.
Таким образом, этот метод всегда возвращает 1 независимо откуда он был вызван.
x равно 1 и z также присваивается 1.
Важно отметить, что f получает свое определение в том месте, где он определен.
Если он определен в том месте, где x равно 1, метод f определяется, чтобы вернуть 1.
И это видно в этом примере.
В этом примере у нас есть два метода: f и g.

g вызывает f, и он вызывает его в контексте, где x равно 0.
И здесь нужно учитывать, что метод f был определен в контексте, где x равно 1.
И мы уже сказали, что метод f всегда возвращает 1 независимо от того, где он вызывается.
Так как здесь x равно 1.
Это называется лексической областью действия или статической областью действия в отличие от динамической области действия.
Большинство языков программирования имеют статическую область действия, в том числе и Java.
Поэтому, как только метод определен, его значение и его поведение, зафиксированы.
Теперь, если мы удалим самое верхнее объявление x, переменная x не определяется при объявлении f.

Следовательно, этот сегмент кода выдаст ошибку во время компиляции.
Далее мы проанализируем взаимосвязь между частично определенными функциями в математике, и методами в Java, которые не определены для некоторых входных значений.
В математике мы изучаем функции, т. е. отображения между множествами значений, где значения области определения X сопоставляются значениям множества Y.
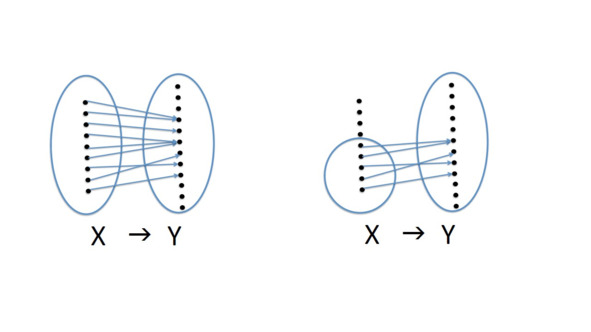
Обычно для всех значений из множества X существуют значения во множестве Y.
Однако может быть случай, когда для некоторых значений X нет отображения, определенного в Y.
В этом случае мы говорим о частично определенной функции.
Если вы хотите избежать частично определенных функций и всегда работать с полными функциями, вы можете выделить в X меньшее множество, где все значения имеют отображение.
Теперь вернемся к Java.
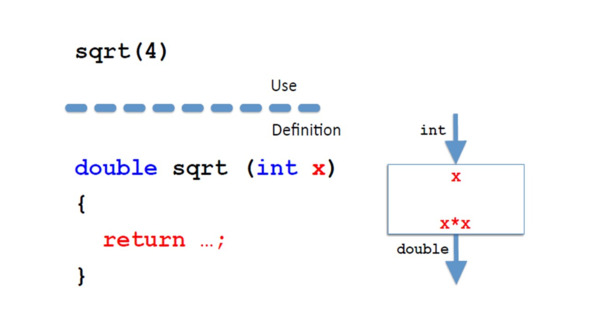
Предположим, мы хотим вычислить квадратный корень из 4.
Здесь есть два результата, плюс 2 и минус 2.
Предположим, что наш метод просто возвращает положительное значение, плюс 2.
Мы всегда можем получить другое решение, добавив знак минус.
Теперь, что произойдет, если мы вызовем метод square с аргументом минус 4?
Мы знаем, что решением в этом случае являются не действительные числа, а мнимые числа.
Таким образом, не существует реального числа, которое может быть предложено в качестве результата метода.
Метод не определен для отрицательных чисел.
В математике мы можем определить функции более подробно.
Мы можем настроить область определения в соответствии с тем, что нам нужно.
Например, мы могли бы сказать, что область определения этой функции не множество целых чисел, а множество натуральных чисел, то есть 0 и положительные целые числа.
Таким образом, функция будет определена для всех значений в этой области определения натуральных чисел.
Но в программировании мы имеем дело с существующими типами.
Теперь, как мы определяем в Java частично определенные функции или частично определенные методы?
Что мы можем сделать в случае метода, который не определен для всех возможных входных значений.
Во-первых, так как возникает ошибка при вызове метода square с отрицательным числом, мы будем ожидать ошибку, и программа должна завершиться с ошибкой.
Это, конечно, не самый удобный способ для решения этой проблемы.
Во-вторых, мы можем проверять значения параметров метода в самом методе или при вызове метода.
Или мы можем перехватить и обработать возникшую ошибку в самом методе или после его вызова, и об этом мы поговорим, когда будем обсуждать исключения Java.







