Яков Перельман
Занимательная механика

Полная версия

Действие и противодействие

Желая открыть дверь, вы тянете её за ручку к себе. Мышца вашей руки, сокращаясь, сближает свои концы: она с одинаковой силой влечёт дверь и ваше туловище одно к другому. В этом случае ясно, что между вашим телом и дверью действуют две силы, приложенные одна к двери, другая – к вашему телу. То же самое, разумеется, происходит и в случае, когда дверь открывается не на вас, а от вас: силы расталкивают дверь и ваше тело.

Рис. 5. Силы (Р, Q, R), действующие на грузик детского воздушного шара. Где силы противодействующие?

То, что мы наблюдаем здесь для силы мускульной, верно для всякой силы вообще независимо от того, какой она природы. Каждое напряжение действует в две противоположных стороны; оно имеет, выражаясь образно, два конца (две силы): один приложен к телу, на которое, как мы говорим, сила действует, другой приложен к телу, которое мы называем действующим. Сказанное принято выражать в механике коротко – слишком коротко для ясного понимания – так: действие равно противодействию.

Смысл этого закона состоит в том, что все силы природы – силы двойные. В каждом случае проявления действия силы вы должны представлять себе, что где-то в ином месте имеется другая сила, равная этой, но направленная в противоположную сторону. Эти две силы действуют непременно между двумя точками, стремясь их сблизить или растолкнуть.

Пусть вы рассматриваете (рис. 5) силы P, Q и R, которые действуют на грузик, подвешенный к детскому воздушному шарику. Тяга Р шара, тяга Q верёвочки и вес R грузика – силы как будто одиночные. Но это лишь отвлечение от действительности; на самом деле для каждой из трёх сил имеется равная ей, но противоположная по направлению сила. А именно сила, противоположная силе Р, приложена к воздушному шарику (рис. 6, сила Р₁); сила, противоположная силе Q, действует на руку; сила, противоположная силе R, приложена в центре земного шара (рис. 6, сила R₁), потому что грузик не только притягивается Землёй, но и сам её притягивает.

Рис. 6. Ответ на вопрос предыдущего рисунка: P₁, Q₁, R₁ – силы противодействующие

Ещё одно существенное замечание. Когда мы спрашиваем о величине натяжения верёвки, концы которой растягиваются силами в 1 Н, мы спрашиваем, в сущности, о цене 10-копеечной почтовой марки. Ответ содержится в самом вопросе: верёвка натянута с силой 1 Н. Сказать «верёвка растягивается двумя силами в 1 Н» или «верёвка подвержена натяжению в 1 Н» – значит выразить буквально одну и ту же мысль. Ведь другого натяжения в 1 Н быть не может, кроме такого, которое состоит из двух сил, направленных в противоположные стороны. Забывая об этом, впадают нередко в грубые ошибки, примеры которых мы сейчас приведём^[10].

Задача о двух лошадях

Две лошади растягивают пружинный безмен^[11] с силой 1000 Н каждая. Что показывает стрелка безмена?

Решение

Многие отвечают: 1000 + 1000 = 2000 Н. Ответ неверен. Силы по 1000 Н, с какими тянут лошади, вызывают, как мы только что видели, натяжение не в 2000, а только в 1000 Н.

Рис. 7. Каждая лошадь тянет с силой 1000 Н. Сколько показывает пружинный безмен?

Поэтому, между прочим, когда магдебургские полушария растягивались 8 лошадьми в одну сторону и 8 в противоположную, то не следует думать, что они растягивались силой 16 лошадей. При отсутствии противодействующих 8 лошадей остальные восемь не произвели бы на полушария ровно никакого действия. Одну восьмёрку лошадей можно было бы заменить просто стеной.

Задача о двух лодках

К пристани на озере приближаются две одинаковые лодки. Оба лодочника подтягиваются с помощью верёвки. Противоположный конец верёвки первой лодки привязан к тумбе на пристани; противоположный же конец верёвки второй лодки находится в руках матроса на пристани, который также тянет верёвку к себе. Все трое прилагают одинаковые усилия. Какая лодка причалит раньше?

Решение

На первый взгляд может показаться, что причалит раньше та лодка, которую тянут двое: двойная сила порождает большую скорость.

Рис. 8. Какая лодка причалит раньше?

Но верно ли, что на эту лодку действует двойная сила? Если и лодочник, и матрос оба тянут к себе верёвку, то натяжение верёвки равно силе только одного из них – иначе говоря, оно таково же, как и для первой лодки. Обе лодки подтягиваются с равной силой и причалят одновременно^[12].

Загадка пешехода и паровоза

Бывают случаи – на практике нередкие, – когда как действующая, так и противодействующая силы приложены в разных местах одного и того же тела. Мускульное напряжение или давление пара в цилиндре паровоза представляют примеры таких сил, называемых внутренними. Особенность их та, что они могут изменять взаимное расположение частей тела, насколько это допускает связь частей, но никак не могут сообщить всем частям тела одно общее движение. При выстреле из ружья пороховые газы, действуя в одну сторону, выбрасывают пулю вперёд. В то же время давление пороховых газов, направленное в противоположную сторону, сообщает ружью движение назад. Двигать вперёд и пулю, и ружьё давление пороховых газов, как сила внутренняя, не может.

Но если внутренние силы не способны перемещать всё тело, то как же движется пешеход? Как движется паровоз? Сказать, что пешеходу помогает трение ног о землю, а паровозу – трение колес о рельсы, не значит еще разрешить загадку. Трение, конечно, совершенно необходимо для движения пешехода и паровоза: известно, что нельзя ходить по очень скользкому льду и что паровоз на скользких рельсах вращает колеса, не двигаясь с места. Но известно и то, что трение – сила пассивная (с. 20), не способная сама по себе порождать движение.

Выходит, что силы, участвующие в движении пешехода и паровоза, не могут заставить их двигаться. Каким же образом движение всё-таки происходит?

Загадка разрешается довольно просто. Две внутренние силы, действуя одновременно, не могут сообщить телу движения, так как действие одной силы уравновешивается действием другой. Но что будет, если некоторая третья сила уравновесит или ослабит действие одной из двух внутренних сил? Тогда ничто не помешает другой внутренней силе двигать тело. Трение и есть та третья сила, которая ослабляет действие одной из внутренних сил и тем даёт другой силе возможность двигать тело.

Для большей ясности обозначим обе внутренние силы буквами F₁ и F₂, а силу трения – буквой F₃. Если величина и направление силы F₃ таковы, что она достаточно ослабляет действие силы F₂, то сила F₁ сможет привести тело в движение. Короче, движение пешехода и паровоза осуществляется потому, что из трёх действующих на тело сил

F₁, F₂, F₃

силы F₂ и F₃ полностью или частью уравновешиваются, и тогда сила F₁ становится действующей.

Инженеры, описывая движение паровоза, предпочитают говорить, не вполне последовательно, что уравновешиваются силы F₁ и F₂, а движет паровоз сила трения F₃. Практически это, впрочем, безразлично, поскольку для движения паровоза необходимо участие и силы пара, и силы трения.

Что значит преодолеть инерцию?

Закончим главу рассмотрением ещё одного вопроса, также зачастую порождающего превратные представления.

Приходится нередко читать и слышать, что для приведения покоящегося тела в движение надо прежде всего преодолеть инерцию этого тела. Мы знаем, однако, что свободное тело нисколько не сопротивляется стремлению силы привести его в движение. Что же тут надо «преодолевать»?

«Преодоление инерции» – не более как условное выражение той мысли, что каждое тело для приведения себя в движение с определённой скоростью требует и определённого промежутка времени. Никакая сила, даже самая большая, не может мгновенно сообщить заданную скорость никакой массе, как бы ни была ничтожна эта масса. Мысль эта замкнута в краткой формуле

ft = mv,

о которой мы будем говорить в следующей главе, но которая, надеюсь, знакома читателю из учебника физики. Ясно, что при t = 0 (время равно нулю) произведение mv (массы на скорость) равно нулю, и, следовательно, скорость равна нулю, так как масса не может равняться нулю. Другими словами, если силе /не дать времени для проявления её действия, она не сообщит телу никакой скорости, никакого движения. Если масса тела велика, потребуется сравнительно большой промежуток времени, чтобы сила сообщила телу заметное движение. Нам будет казаться, что тело начинает двигаться не сразу, что оно словно противится действию силы. Отсюда и сложилось ложное представление о том, что сила, прежде чем заставить тело двигаться, должна «преодолеть его инерцию», его косность (буквальный смысл слова «инерция»).

Железнодорожный вагон

Один из читателей просит меня разъяснить вопрос, который, в связи с только что сказанным, возник, вероятно, у многих: «Почему сдвинуть железнодорожный вагон с места труднее, чем поддерживать движение вагона, уже катящегося равномерно?»

Не только труднее, прибавлю я, но и вовсе невозможно, если прилагать небольшое усилие. Чтобы поддерживать равномерное движение пустого товарного вагона по горизонтальному пути, достаточно, при хорошей смазке, усилия в 150 Н. Между тем такой же неподвижный вагон не удаётся сдвинуть с места силой меньшей 600 Н.

Причина не только в том, что приходится в течение первых секунд затрачивать силу на приведение вагона в движение с заданной скоростью (затрата эта сравнительно невелика), причина кроется главным образом в условиях смазки стоящего вагона. В начале движения смазка ещё не распределена равномерно по всему подшипнику, и оттого заставить вагон двигаться тогда очень трудно. Но едва колесо сделает первый оборот, условия смазки сразу значительно улучшаются, и поддерживать дальнейшее движение становится несравненно легче.

Глава 2
Сила и движение

Справочная таблица по механике

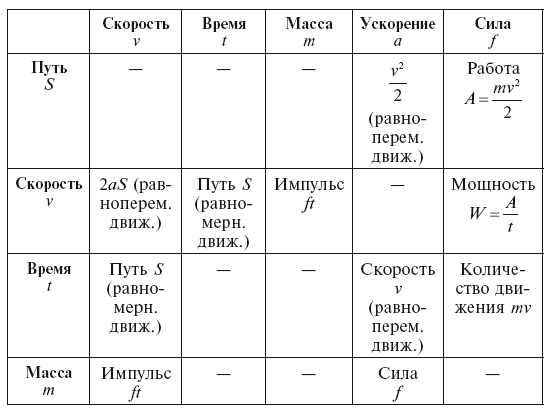
«Никакое человеческое знание не может притязать на название истинной науки, если оно не пользуется математическими доказательствами», – писал в XVI веке Леонардо да Винчи. Это было верно уже в младенческие годы науки; ещё правильнее такое утверждение для наших дней. В настоящей книге нам не раз придётся обращаться к формулам из механики. Для читателей хотя и проходивших механику, но забывших эти соотношения, дана здесь небольшая табличка-справочник, помогающая восстановить в памяти важнейшие формулы. Она составлена по образцу пифагоровой таблицы умножения: на пересечении двух граф отыскивается то, что получается от умножения величин, написанных по краям. (Обоснование этих формул читатель найдет в учебниках механики.)

Покажем на нескольких примерах, как пользоваться табличкой.

Умножая скорость v равномерного движения на время t, получаем путь S (формула S = vt).

Умножая силу f на путь S, получаем работу А, которая в то же время равна и полупроизведению массы m на квадрат скорости 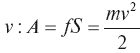.^[13]

Подобно тому как с помощью таблицы умножения можно узнавать результаты деления, так и из нашей таблички можно извлечь, например, следующие соотношения.

Скорость v равнопеременного движения, делённая на время t, равна ускорению а (формула )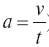

Сила f, делённая на массу m, равна ускорению а; делённая же на ускорение а, равна массе m:

Пусть для решения механической задачи вам потребовалось вычислить ускорение. Вы составляете по табличке все формулы, содержащие ускорение, прежде всего формулы:

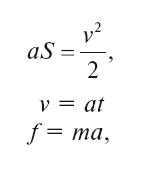
а затем и формулу

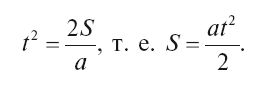
Среди них ищете ту, которая отвечает условиям задачи.

Если пожелаете иметь все уравнения, с помощью которых может быть определена сила, табличка предложит вам на выбор:

fS= А (работа)

fv = W (мощность)

ft = mv (количество движения)

f = mа.

Не надо упускать из виду, что вес (Р) есть тоже сила, поэтому наряду с формулой f = mа в нашем распоряжении имеется и формула Р = mg, где g – ускорение силы тяжести близ земной поверхности. Точно так же из формулы fS = А следует, что Ph = А – для тела весом Р, поднятого на высоту h.

Пустые клетки таблицы показывают, что произведения соответствующих величин не имеют в механике никакого смысла.

Ещё важное замечание. Формулы механики полезны только в руках того вычислителя, который твёрдо знает, в каких мерах надо выразить входящие в них величины. Если, вычисляя работу по формуле А = fS, вы выразите силу f в ньютонах, а путь S – в сантиметрах, то получите величину работы в редко употребительных единицах – в ньютоно-сантиметрах и, конечно, легко можете запутаться. Чтобы получился надлежащий результат, сила должна быть выражена в ньютонах, а путь – в метрах, тогда работа получится в ньютоно-метрах, или, по-другому, в джоулях. Но вы можете выразить силу и в динах, а путь в сантиметрах, тогда результат покажет число эргов работы (дина – сила, равная 1/100 000 ньютона, т. е. 100 мН) – дино-сантиметров.

Точно так же равенство f = mа даст силу в динах только тогда, когда масса выражена в граммах, а ускорение – в сантиметрах в секунду за секунду.

Умению выбирать единицы мер и безошибочно определять, в каких мерах получился результат, нельзя научиться в четверть часа. Кто этим умением ещё не обладает, тому следует во всех случаях пользоваться мерами системы «сантиметр – грамм – секунда» (СГС), а полученный результат, если нужно, переводить в другие меры^[14].

Эти практические мелочи очень существенны, незнание их зачастую приводит к самым нелепым ошибкам.

Отдача огнестрельного оружия

В качестве примера применения нашей таблицы рассмотрим отдачу ружья. Пороховые газы, выбрасывающие своим напором пулю в одну сторону, отбрасывают в то же время и ружьё в обратную сторону, порождая всем известную отдачу. С какой скоростью движется отдающее ружьё? Вспомним закон равенства действия и противодействия. По этому закону давление пороховых газов на ружьё должно быть равно давлению пороховых газов на пулю, выбрасываемую пулю. При этом обе силы действуют одинаковое время. Заглянув в таблицу, находим, что произведение силы (f) на время (t) равно «количеству движения» mv, т. е. произведению массы m на её скорость v:

ft = mv.

Так как ft для пули и для ружья одинаково, то должны быть одинаковы и количества движения. Если m – масса пули, v – её скорость, M – масса ружья, w – его скорость, то согласно сейчас сказанному

mv = Mw,

откуда

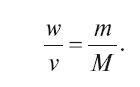
Подставим в эту пропорцию числовые значения её членов. Масса пули старой военной винтовки – 9,6 г, скорость её при вылете – 880 м/с, масса винтовки – 4500 г. Значит,

Следовательно, скорость ружья примерно равна 1,9 м/с. Нетрудно вычислить, что отдающее ружьё несёт с собой в 470 раз меньшую «живую силу» 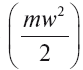, нежели пуля; это значит, что разрушительная энергия ружья при отдаче в 470 раз меньше, нежели пули, хотя – заметим это! – количество движения для обоих тел одинаково. Неумелого стрелка отдача может всё же опрокинуть и даже поранить.

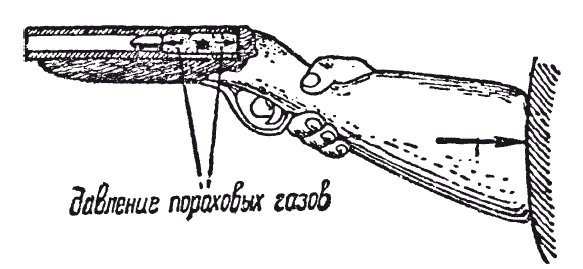
Рис. 9. Почему ружьё при выстреле отдаёт?

Для нашей старой полевой скорострельной пушки, весящей 2000 кг и выбрасывающей 6-килограммовые снаряды со скоростью 600 м/с, скорость отдачи примерно такая же, как и у винтовки – 1,9 м/с. Но при значительной массе орудия энергия этого движения в 450 раз больше, чем для винтовки и почти равна энергии ружейной пули в момент её вылета. Старинные пушки откатывались отдачей с места назад. В современных орудиях скользит назад только ствол, лафет же остаётся неподвижным, удерживаемый упором (сошником) на конце хобота. Морские орудия (не вся орудийная установка) при выстреле откатываются назад, но, благодаря особому приспособлению, сами после отката возвращаются на прежнее место.

Читатель, вероятно, заметил, что в наших примерах тела, наделённые равными количествами движения, обладают далеко не одинаковой кинетической энергией.

В этом, разумеется, нет ничего неожиданного: из равенства

mv = Mw

вовсе не следует, что

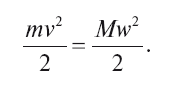
Второе равенство верно лишь в том случае, когда v = w (в этом легко убедиться, разделив второе равенство на первое). Между тем среди людей, не изучавших механику систематически, весьма распространено неправильное убеждение, будто равенство количеств движения (а значит, и равенство импульсов) обусловливает собой равенство кинетической энергии. Многие изобретатели-самоучки, как я заметил, исходят из того, что равным импульсам соответствуют равные количества работы. Это ведёт, конечно, к плачевным неудачам и лишний раз доказывает необходимость для изобретателя хорошо усвоить основы теоретической механики.

Знание обиходное и научное

При изучении механики поражает то, что во многих весьма простых случаях наука эта резко расходится с обиходными представлениями. Вот показательный пример. Как должно двигаться тело, на которое неизменно действует одна и та же сила? Здравый смысл подсказывает, что такое тело должно двигаться всё время с одинаковой скоростью, т. е. равномерно. И наоборот, если тело движется равномерно, то в обиходе это считается признаком того, что на тело действует всё время одинаковая сила. Движение телеги, паровоза и т. и. как будто подтверждает это.

Рис. 10

Механика говорит, однако, совершенно другое. Она учит, что постоянная сила порождает движение не равномерное, а ускоренное, так как к скорости, ранее накопленной, сила непрерывно добавляет новую скорость. При равномерном же движении тело вовсе не находится под действием силы, иначе оно двигалось бы неравномерно (см. с. 20).

Неужели же обиходные наблюдения так грубо ошибочны?

Нет, они не вполне ошибочны, но относятся к весьма ограниченному кругу явлений. Обиходные наблюдения делаются над телами, перемещающимися в условиях трения и сопротивления среды. Законы же механики имеют в виду тела, движущиеся свободно. Чтобы тело, движущееся с трением, обладало постоянной скоростью, к нему действительно надо приложить постоянную силу. Но сила тратится здесь не на то, чтобы двигать тело, а лишь на то, чтобы преодолевать трение, т. е. создать для тела условия свободного движения. Вполне возможны поэтому случаи, когда тело, движущееся с трением равномерно, находится под действием постоянной силы.

Мы видим, в чём грешит обиходная механика: её утверждения почерпнуты из недостаточного материала. Научные обобщения имеют более широкую базу. Законы научной механики выведены из движения не только телег и паровозов, но также планет и комет. Чтобы делать правильные обобщения, надо расширить поле наблюдений и очистить факты от случайных обстоятельств. Только так добытое знание раскрывает глубокие корни явлений и может быть плодотворно применено на практике.

В дальнейшем мы рассмотрим ряд явлений, где отчётливо выступает связь между величиной силы, двигающей свободное тело, и величиной приобретаемого им ускорения, связь, которая устанавливается уже упоминавшимся вторым законом Ньютона. Это важное соотношение, к сожалению, смутно усваивается при школьном прохождении механики. Примеры взяты в обстановке фантастической, но сущность явления выступает от этого ещё отчетливее.

Пушка на Луне

Задача

Артиллерийское орудие сообщает снаряду на Земле начальную скорость 900 м/с. Перенесите его мысленно на Луну, где все тела становятся в 6 раз легче. С какой скоростью снаряд покинет там это орудие? (Различие, обусловленное отсутствием на Луне атмосферы, оставим без внимания.)

Решение

На вопрос этой задачи часто отвечают, что так как сила взрыва на Земле и на Луне одинакова, а действовать на Луне приходится ей на вшестеро более лёгкий снаряд, то сообщённая скорость должна быть там в 6 раз больше, чем на Земле: 900 × 6 = 5400 м/с. Снаряд вылетит на Луне со скоростью 5,4 км/с.

Подобный ответ при кажущемся его правдоподобии совершенно неверен.

Между силой, ускорением и весом вовсе не существует той связи, из какой исходит приведённое рассуждение. Формула механики, являющаяся математическим выражением второго закона Ньютона, связывает силу и ускорение с массой, а не с весом: f = ma. Но масса снаряда нисколько на Луне не изменилась: она там та же, что и на Земле; значит, и ускорение, сообщаемое снаряду силой взрыва, должно быть на Луне такое же, как и на Земле: а при одинаковых ускорениях и времени – одинаковы и скорости (согласно формуле v = at).

Итак, пушка на Луне выбросила бы снаряд точно с такой же начальной скоростью, как и на Земле. Другое дело, как далеко или как высоко залетел бы на Луне этот снаряд. В этом случае ослабление тяжести имеет уже существенное значение.

Например, высота отвесного подъёма снаряда, покинувшего на Луне пушку со скоростью 900 м/с, определится из формулы

которую мы находим в справочной табличке (с. 31). Так как ускорение силы тяжести на Луне в 6 раз меньше, чем на Земле, т. е. 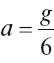, то формула получает вид:

Отсюда пройденный снарядом отвесный путь

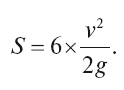
На Земле же (при отсутствии атмосферы):

Значит, на Луне пушка закинула бы ядро в 6 раз выше, чем на Земле (сопротивление воздуха мы не принимали во внимание), несмотря на то что начальная скорость снаряда в обоих случаях одинакова.