
Асват Дамодаран
Инвестиционная оценка. Инструменты и методы оценки любых активов
ПОЧЕМУ ФИНАНСОВЫЕ ИНВЕСТОРЫ ПРЕДПОЛОЖИТЕЛЬНО ДИВЕРСИФИЦИРОВАНЫ?
Утверждение, что диверсификация снижает подверженность инвестора риску, понятно и на интуитивном уровне, и с точки зрения статистики, однако модели риска и доходов в финансах идут дальше. Они рассматривают риск с точки зрения инвестора, который может продать акции в любой момент времени. Такой инвестор называется финансовым. При этом доказывается, что этот инвестор, устанавливающий цены на инвестиции, имеет хорошую диверсификацию. Таким образом, единственный риск, который его волнует, – это риск, добавляемый к диверсифицированному портфелю, или рыночный риск. Этот аргумент легко обосновать. Риск, характеризующий инвестицию, всегда будет оцениваться выше инвестором, не обладающим диверсификацией, по сравнению с тем, кто ею обладает, поскольку последний не принимает на себя специфический риск фирмы, а первый – принимает. Если у обоих инвесторов одинаковые ожидания относительно будущих доходов и денежных потоков, приходящихся на актив, то «диверсифицированный» инвестор пожелает заплатить более высокую цену за этот актив, поскольку он оценивает риск как более низкий. Следовательно, со временем актив окажется в портфелях «диверсифицированных» инвесторов.
Данное соображение – весьма действенное доказательство, особенно на рынках, где торговля активами ничем не затруднена и связана с низкими издержками. Таким образом, это утверждение хорошо работает применительно к акциям, обращающимся в США, поскольку инвесторы могут стать «диверсифицированными» при низких издержках. Кроме того, значительная доля торговли акциями в США осуществляется институциональными инвесторами, которые, как правило, хорошо «диверсифицированы». Обоснование оказывается более проблематичным, если торговля активами связана с трудностями или предполагает высокие издержки. На таких рынках финансовый инвестор может быть плохо «диверсифицированным», а потому специфический риск фирмы способен сохранять свое влияние при рассмотрении отдельных инвестиций. Например, в большинстве стран недвижимостью владеют «недиверсифицированные» инвесторы, которые хранят значительную часть своих сбережений в этих инвестициях.
Модель оценки финансовых активов предполагает, что транзакционные издержки отсутствуют, все активы обращаются на открытом рынке, а инвестиции бесконечно делимы (т. е. можно купить любую долю от единицы данного актива). Кроме того, предполагается возможность свободного доступа к одной и той же информации для всех инвесторов, и из этого следует, что инвесторы не могут выявить на рынке переоцененные и недооцененные активы. Все эти предположения позволяют инвестору быть «диверсифицированным» без дополнительных издержек. В предельном случае их портфели не только будут включать каждый из обращающихся на рынке активов, но и, помимо всего прочего, рискованные активы будут обладать одинаковыми весами (на основе их рыночной стоимости).
Тот факт, что в данный портфель включаются все обращающиеся на рынке активы, служит основанием для того, чтобы его называли рыночным портфелем. В этом нет ничего удивительного, учитывая выигрыши от диверсификации и отсутствие транзакционных издержек в модели оценки финансовых активов. Если диверсификация сокращает степень подверженности риску на уровне фирмы и отсутствуют издержки, связанные с добавлением дополнительных активов в портфель, то логическим ограничением диверсификации станет владение небольшой долей каждого из активов, обращающихся в экономике. Если это определение кажется слишком абстрактным, представим себе, что рыночный портфель представляет собой очень хорошо диверсифицированный взаимный фонд, который держит акции и реальные активы. В модели САРМ все инвесторы будут держать комбинации, состоящие из более рискованного актива и этого взаимного фонда[24].
Портфели инвесторов в САРМ. Если все инвесторы на рынке имеют одинаковые рыночные портфели, то каким образом выражается реакция инвесторов, обусловленная неприятием риска в совершаемых ими инвестициях? В модели оценки финансовых активов, когда инвесторы при распределении средств решают: сколько им следует вложить в безрисковый актив, а сколько – в рыночный портфель, они опираются на свои предпочтения в области риска. Инвесторы, избегающие риска, могут принять решение вложить все свои сбережения в безрисковый актив. Инвесторы, желающие принять на себя больше риска, вложат значительную часть своих сбережений, или даже все, в рыночный портфель. Инвесторы, уже вложившие все свои средства в рыночный портфель и, тем не менее, желающие принять на себя еще больше риска, могли бы добиться этого, заняв средства по безрисковой ставке и инвестировав их в тот же самый рыночный портфель, следуя примеру всех остальных.
Данные предположения основываются на двух дополнительных допущениях. Во-первых, существует безрисковый актив, ожидаемый доход которого известен с абсолютной определенностью. Во-вторых, инвесторы могут ссужать и занимать средства по безрисковой ставке для достижения оптимальности размещения средств. В то время как ссуда по безрисковой ставке не доставляет особых проблем (индивиду для этого достаточно приобрести казначейские векселя или казначейские облигации), получение ссуд по безрисковой ставке может оказаться куда более затруднительным для отдельного лица. Существуют версии модели CAPM, позволяющие несколько смягчить эти допущения и, тем не менее, получить выводы, совместимые с моделью.
Измерение рыночного риска отдельного актива. Риск любого актива для инвестора – это риск, добавляемый данным активом к портфелю инвестора в целом. В мире САРМ, где все инвесторы владеют рыночным портфелем, риск отдельного актива для инвестора – это риск, который данный актив добавляет к рыночному портфелю. На интуитивном уровне понятно, что если движение актива происходит независимо от рыночного портфеля, то этот актив не добавит слишком уж много риска к рыночному портфелю. Другими словами, большая часть риска данного актива является специфическим риском фирмы, а потому может быть диверсифицирована. С другой стороны, если стоимость актива имеет тенденцию к росту одновременно с повышением стоимости портфеля, равно как и тенденцию к падению при снижении стоимости рыночного портфеля, то актив увеличивает риск портфеля. Такой актив обладает в большей степени рыночным риском и в меньшей – специфическим риском фирмы. Статистически, добавленный риск измеряется ковариацией актива с рыночным портфелем.
Измерение недиверсифицируемого риска. В мире, где инвесторы держат комбинацию только двух активов: безрискового актива и рыночного портфеля, риск любого отдельного актива будет измеряться по отношению к рыночному портфелю. В частности, риск какого-либо актива будет риском, добавляемым им к рыночному портфелю. Чтобы получить адекватную меру для этого добавляемого риска, предположим, что σ2 есть дисперсия рыночного портфеля до того, как в него включили новый актив, а дисперсия отдельного актива, добавляемого к портфелю, равна σi2. Вес данного актива в рыночной стоимости портфеля составляет wi, а ковариация доходов между отдельным активом и рыночным портфелем равна σim. Дисперсию рыночного портфеля до и после включения в портфель отдельного актива можно записать следующим образом:

Вес рыночной стоимости любого отдельного актива в рыночном портфеле может быть небольшим, поскольку рыночный портфель включает в себя все активы, обращающиеся в экономике. Следовательно, первый член (ковариацию σim) в качестве меры риска, добавляемого активом i.
Стандартизация ковариации. Ковариация измеряется в процентах, поэтому трудно вынести решение по поводу относительного риска инвестиции, основываясь на ее значении. Другими словами, знание ковариации компании Boeing с рыночным портфелем (составляющей 55 %) не дает нам подсказки, в большей или в меньшей степени рискованна компания по сравнению со средним активом. По этой причине мы стандартизируем меру риска путем деления ковариации каждого актива с рыночным портфелем на дисперсию рыночного портфеля. Это позволяет получить показатель риска, который называется коэффициентом бета (beta) данного актива:
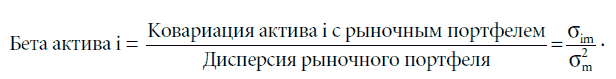
Поскольку ковариация рыночного портфеля с самим собой является его дисперсией, бета рыночного портфеля (как и его среднего актива) равна 1. Активы, чья рискованность выше среднего уровня (если использовать эту меру риска), будут иметь коэффициент бета выше единицы, а активы, которые безопаснее среднего уровня, будут обладать бетой менее единицы. У безрисковых активов коэффициент бета равен нулю.
Получение ожидаемых доходов. Факт удержания каждым инвестором некоторой комбинации безрискового актива и рыночного портфеля приводит к заключению, что ожидаемый доход на актив линейно зависит от беты актива. В частности, ожидаемый доход на актив можно записать как функцию безрисковой ставки и беты этого актива:
E(Ri) = Rf + Pi [E(Rm)-Rf],
где E(Ri) = ожидаемая доходность актива i;
Rf = безрисковая ставка;
E(Rm) = ожидаемая доходность на рыночный портфель;
Pi = коэффициент бета актива i.
Для использования модели оценки финансовых активов нам необходимо иметь три входные величины. Следующая глава будет посвящена детальному разбору процесса оценки, поэтому пока только заметим, что каждая из этих входных величин оценивается следующим образом:
• Безрисковый актив определяется как актив, относительно которого инвестору с абсолютной определенностью известна ожидаемая доходность для временного горизонта анализа.
• Премия за риск является премией, запрашиваемой инвесторами за инвестирование в рыночный портфель, включающий все рисковые активы на рынке, вместо инвестирования в безрисковый актив.
• Коэффициент бета, который определяется как ковариация актива, поделенная на дисперсию рыночного портфеля, измеряет риск, добавляемый инвестицией к рыночному портфелю.
Таким образом, в модели оценки финансовых активов весь рыночный риск охватывается одним коэффициентом бета, измеренным по отношению к рыночному портфелю, который, хотя бы теоретически, должен содержать все обращающиеся на рынке активы пропорционально их рыночной стоимости.
Модель арбитражной оценки. Ограничивающие предположения, касающиеся транзакционных издержек и получения информации в модели оценки финансовых активов, а также зависимость модели от рыночного портфеля на протяжении длительного времени воспринимались академическими кругами и специалистами-практиками со скептицизмом. Росс (Ross, 1976) предложил альтернативную модель для измерения риска, которая называется моделью арбитражной оценки (arbitrage pricing model – APM).
Предположения. Если инвесторы могут инвестировать без риска и зарабатывать больше, чем по безрисковой ставке, то это означает, что они нашли возможность арбитража[25]. Предположение, лежащее в основе модели арбитражной оценки, заключается в том, что инвесторы пользуются выгодами возможности совершения арбитража и устраняют их в процессе торгов. Если два портфеля в одинаковой степени подвержены риску, но предлагают различный ожидаемый доход, то инвесторы приобретут портфель с более высоким ожидаемым доходом и продадут портфель с меньшим ожидаемым доходом. Заработанная разница будет безрисковой прибылью. Для предотвращения возможности арбитража два портфеля должны создавать одинаковые ожидаемые доходы.
Подобно модели оценки финансовых активов, модель арбитражной оценки начинает с разделения риска на специфический риск фирмы и рыночный риск. Как и в модели оценки финансовых активов, специфический риск фирмы охватывает информацию, которая влияет в основном на саму фирму. Рыночный риск касается многих или всех фирм и предполагает непредвиденные изменения в определенном числе экономических переменных, включая ВВП, инфляцию и процентные ставки. Включив оба типа риска в модель доходности, мы получаем:
R= E(R) + m + ε,
где R – фактическая доходность, E(R) – ожидаемая доходность, m – компонент непредвиденного риска в масштабе всего рынка, ε – компонент отдельной фирмы. Таким образом, фактический доход может отличаться от ожидаемого дохода либо по причине рыночного риска, либо вследствие специфического риска фирмы.
Источники рыночного риска. Хотя и модель оценки финансовых активов, и модель арбитражной оценки различают риск отдельной фирмы и рыночный риск, они измеряют рыночный риск по-разному. Модель САРМ предполагает, что рыночный риск полностью охватывается рыночным портфелем, в то время как модель арбитражной оценки допускает множество источников рыночного риска, измеряя чувствительность инвестиций к изменениям в каждом идентифицированном источнике. Вообще говоря, рыночный компонент непредвиденных доходов можно разложить на экономические факторы:
R = E(R) + m + ε = R + (Β1F1 + Β2F2 + … + ΒnFn) + ε,
где Βj = чувствительность инвестиции к непредвиденным изменениям в факторе j;
где Fj = чувствительность инвестиции к непредвиденным
Отметим, что измерение чувствительности инвестиции к любому макроэкономическому фактору принимает форму коэффициента бета, который называется фактором бета. В действительности, данный фактор бета во многом сходен с рыночным коэффициентом бета в модели САРМ.
Результаты диверсификации. Преимущества диверсификации обсуждались ранее в контексте разделения на рыночный и специфический риск фирмы. Основные положения этой дискуссии связаны с устранением этой диверсификации специфического риска фирмы. Модель арбитражной оценки привлекает ту же самую аргументацию и приводит к выводу, что доходность портфеля не будет содержать компонент непредвиденных доходов отдельной фирмы. Доход портфеля можно записать как сумму двух средневзвешенных – ожидаемого дохода портфеля и рыночных факторов:

Ожидаемые доходы и коэффициенты бета. Заключительным шагом в этом процессе является оценка ожидаемого дохода как функции только что определенных коэффициентов бета. Заметим сначала, что бета портфеля является средневзвешенной величиной коэффициентов бета различных активов, входящих в портфель. Данная особенность, в сочетании с отсутствием возможности арбитража, приводит к заключению, что ожидаемые доходы находятся в линейной зависимости от коэффициентов бета. Чтобы понять причины этого, предположим, что существуют только один фактор и три портфеля. Коэффициент бета портфеля А равен 2,0, а ожидаемый доход – 20 %. Коэффициент бета портфеля В равен 1,0, а ожидаемый доход – 12 %. Портфель С имеет коэффициент бета, равный 1,5, а ожидаемый доход составляет 14 %. Отметим также, что инвесторы могут вложить половину своего состояния в портфель А, а другую половину – в портфель В, что создаст портфель с коэффициентом бета, равным 1,5, и ожидаемым доходом 16 %. Соответственно, ни один инвестор не станет держать портфель С, пока стоимость этого портфеля не упадет и ожидаемый доход не повысится до 16 %. По тем же причинам ожидаемые доходы каждого портфеля должны находиться в линейной зависимости от коэффициента бета. Если бы этой зависимости не было, то мы смогли бы скомбинировать два других портфеля – один с более высоким коэффициентом бета, а другой с более низким, чтобы добиться более высоких доходов по сравнению с исходным портфелем. Тем самым мы заработали бы более высокий доход, чем тот, который приносит рассматриваемый портфель, создавая возможность для арбитража. Данный аргумент можно распространить на ситуацию с множественными факторами и тем же результатом. Следовательно, ожидаемый доход на актив можно записать следующим образом:

Элементы в квадратных скобках можно рассматривать как премии за риск каждого фактора в модели.
Модель оценки финансовых активов можно рассматривать как особый случай модели арбитражной оценки, где присутствует только один экономический фактор, создающий доходы в масштабах всего рынка, и этим фактором является рыночный портфель.
E(R) = Rf + Βm[E(Rm)-Rf].
Модель арбитражной оценки на практике. Модель арбитражной оценки позволяет оценить коэффициенты бета для каждого фактора и премии за риск по факторам в дополнение к безрисковой ставке. На практике они обычно оцениваются при помощи исторических данных по доходам, приходящимся на актив, и факторного анализа. На интуитивном уровне понятно, что в факторном анализе мы изучаем исторические данные на основе исторических образов, характерных скорее для значительных групп активов (чем для одного сектора или нескольких активов). Факторный анализ дает два итоговых показателя:
1. Позволяет определить число общих факторов, влияющих на исторические данные по доходам.
2. Дает возможность измерить коэффициент бета каждой инвестиции относительно любого из общих факторов и обеспечивает оценку фактических премий за риск, заработанных каждым фактором.
Тем не менее факторный анализ не занимается идентификацией факторов с экономических позиций. Как правило, в модели арбитражной оценки рыночный риск измеряется по отношению к множеству не поддающихся спецификации макроэкономических переменных. При этом чувствительность инвестиции соотносится с каждым фактором, измеренным при помощи коэффициента бета. Количество факторов риска, коэффициенты бета для факторов, премии за факторы риска – все эти величины можно оценить при помощи факторного анализа.
Многофакторные модели для риска и доходности. Отказ от идентификации факторов в модели арбитражной оценки, по всей вероятности, можно оправдать, обращаясь к статистическим методам, но, вместе с тем, интуиция подсказывает, что это свидетельствует о слабости подобного подхода. Решение кажется простым: заменить неопределяемые статистические факторы специальными экономическими факторами, и результирующая модель будет обладать экономической основой, вместе с тем сохраняя в себе многие достоинства модели арбитражной оценки. Именно на это и нацелены многофакторные модели.
Создание многофакторной модели. Как правило, многофакторные модели основаны на исторических данных, а не на экономическом моделировании. Как только в модели арбитражной оценки выявлено определенное количество факторов, их поведение можно выяснить с помощью данных. Поведение неназванных факторов во времени можно сравнить с поведением макроэкономических переменных за тот же период с целью проверки, коррелируют ли во времени какие-либо из переменных с идентифицированными факторами.
Например, Чен, Ролл и Росс (Chen, Roll and Ross, 1986) предполагают, что с факторами, полученными при помощи факторного анализа, в значительной степени коррелируют следующие макроэкономические переменные: промышленная продукция, изменения размера премии за дефолт, сдвиги во временной структуре, непредвиденная инфляция и изменения в фактической доходности. Затем можно выяснить корреляцию этих переменных с доходами (что даст нам модель ожидаемых доходов), а также с коэффициентами бета отдельных фирм, рассчитанными по отношению к каждой переменной.

Издержки перехода от модели арбитражной оценки к макроэкономическим многофакторным моделям можно отнести к ошибкам, возникающим при идентификации факторов. Экономические факторы в модели могут со временем изменяться, как и премия за риск, связанная с каждым из них. Например, изменения цен на нефть оставались в 1970-е годы важным экономическим фактором, определяющим ожидаемые доходы, однако в другие периоды времени они не были столь важны. Использование ошибочных факторов или игнорирование важных факторов в многофакторной модели может привести к недостоверным оценкам ожидаемого дохода.
В конечном итоге, многофакторные модели, подобно моделям арбитражной оценки, предполагают, что рыночный риск может быть учтен лучше, если использовать множество экономических факторов и коэффициенты бета, соотнесенные с каждым из них. В отличие от модели арбитражной оценки, многофакторные модели нацелены на идентификацию макроэкономических факторов, определяющих рыночный риск.
Регрессия, или приближенные модели. Все описанные модели начинают с определения рыночного риска в широком смысле, а затем развивают модели, оценивающие этот рыночный риск наилучшим образом. Но все они извлекают свои показатели рыночного риска (бета) из анализа исторических данных. Существует целевой класс моделей риска и доходности, которые начинают с доходов и пытаются объяснить различия в этих доходах, приходящихся на разные акции, в течение длительного временного периода. Для этого используются такие характеристики, как рыночная стоимость фирмы или мультипликаторы, включающие в себя цену[26]. Сторонники этих моделей доказывают, что если доходность некоторых инвестиций выше, чем у других, то и рискованность их должна оказаться выше. Следовательно, мы можем взглянуть на характеристики, объединяющие эти высокодоходные инвестиции, и принять их в качестве косвенных или приближенных показателей рыночного риска.
Фама и Френч (Fama and French, 1992) в своем исследовании модели оценки финансовых активов, получившем широкое признание, отметили, что фактические доходы за период 1963–1990 гг. сильно коррелировали с мультипликаторами «балансовая стоимость/цена»[27] и размером. Высокодоходные инвестиции в этот период, как правило, были связаны с вложениями в компании с низкой рыночной капитализацией и высокими мультипликаторами «балансовая стоимость/цена». Фама и Френч предположили, что эти показатели можно использовать в качестве приближенных оценок риска, и вывели следующую регрессию для ежемесячных доходов на акции, обращающиеся на Нью-Йоркской фондовой бирже (New York Stock Exchange – NYSE):
Rt = 1,77 % – 0,11ln (MV)+0,35ln (BV/MV),
где ln = натуральный логарифм;
MV = рыночная стоимость собственного капитала;
BV/MV = балансовая стоимость/рыночная стоимость собственного капитала.
Значения рыночной стоимости собственного капитала и мультипликатора «BV/MV» для отдельных фирм, принятые в качестве значений для регрессионных переменных, должны давать ожидаемый ежемесячный доход.



